题目内容
动直线x=a与函数f(x)=2
sin
cos
和g(x)=
cosx的图象分别交于A、B两点,则AB的最大值为 .
| 2 |
| x |
| 2 |
| x |
| 2 |
| 2 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:
分析:利用倍角公式把函数f(x)化积,由A,B两点的横坐标相同,把纵坐标作差后取绝对值,求出纵坐标作差后取绝对值的最大值得答案.
解答:
解:f(x)=2
sin
cos
=
sinx,g(x)=
cosx,
动直线x=a与函数f(x)和g(x)的图象分别交于A、B两点,
则A,B的横坐标相同,∴AB的距离即为两点纵坐标差的绝对值.
则|AB|=|
sinx-
cosx|=
|
sin(x-
)|=2|sin(x-
)|.
∴AB的最大值为:2.
故答案为:2.
| 2 |
| x |
| 2 |
| x |
| 2 |
| 2 |
| 2 |
动直线x=a与函数f(x)和g(x)的图象分别交于A、B两点,
则A,B的横坐标相同,∴AB的距离即为两点纵坐标差的绝对值.
则|AB|=|
| 2 |
| 2 |
| 2 |
| 2 |
| π |
| 4 |
| π |
| 4 |
∴AB的最大值为:2.
故答案为:2.
点评:本题考查了三角函数中的恒等变换的应用,考查了数学转化思想方法,训练了与三角函数有关的最值得求法,是中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)在x=
处取得最小值,则( )
| π |
| 4 |
A、f(x+
| ||
B、f(x+
| ||
C、f(x-
| ||
D、f(x-
|
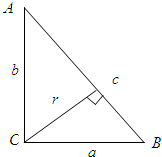 设直角△ABC的直角边BC=a,AC=b,斜边AB=c,且a<b,现分别以直线BC,AC和AB为轴将直角△绕轴旋转一周,所得三个旋转体体积分别为V1,V2和V3,试比较V1,V2,V3的大小.
设直角△ABC的直角边BC=a,AC=b,斜边AB=c,且a<b,现分别以直线BC,AC和AB为轴将直角△绕轴旋转一周,所得三个旋转体体积分别为V1,V2和V3,试比较V1,V2,V3的大小.