题目内容
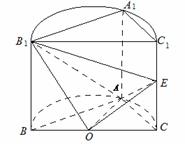
如图,已知平面![]() 是圆柱的轴截面(经过圆柱的轴的截面),
是圆柱的轴截面(经过圆柱的轴的截面),
BC是圆柱底面的直径,O为底面圆心,E为母线![]() 的中点,已知
的中点,已知![]()
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
(3)求三棱锥![]() 的体积.
的体积.
 |
解: 依题意可知, ![]() 平面ABC,∠
平面ABC,∠![]() =90°,
=90°,![]() ,∴
,∴![]()
(I)∵![]() ,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
因为![]() =
=![]() ,则
,则![]() ,∴
,∴![]()
∴B1O⊥EO,
∴![]() ⊥平面
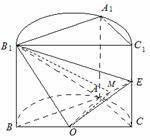
⊥平面![]() ;(II)过O做OM⊥AE于点M,连接B1M,
;(II)过O做OM⊥AE于点M,连接B1M,
∵B1O⊥平面AEO,可证B1M⊥AE,
∴∠B1MO为二面角B1—AE—O的平面角,
C1C⊥平面ABC,AO⊥OC,可证EO⊥AO,
在Rt△AEO中,可求![]() ,
,
在Rt△B1OM中,∠B1OM=90°,∴![]()
∴二面角B1—AE—O的余弦值为![]()
(Ⅲ)因为AB=AC,O为BC的中点,所以![]()
又平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() , 故
, 故![]() 是三棱锥
是三棱锥![]() 的高
的高
∴![]()

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 (2012•青州市模拟)如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4.
(2012•青州市模拟)如图,已知平面BCC1B1是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线CC1的中点,已知AB=AC=AA1=4. 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线 的中点,已知
的中点,已知
 ⊥平面
⊥平面 ;
; 的余弦值.
的余弦值. 的体积.
的体积. 
 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线 的中点,已知
的中点,已知
 ⊥平面
⊥平面 ;
; 的余弦值.
的余弦值. 的体积.
的体积.