题目内容
如图4,已知平面 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线 的中点,已知
的中点,已知
(I))求证: ⊥平面
⊥平面 ;
;
(II)求二面角 的余弦值.
的余弦值.
(Ⅲ)求三棱锥 的体积.
的体积.

【答案】
(I))见解析(II) (Ⅲ)8
(Ⅲ)8
【解析】解:依题意可知,  平面ABC,∠
平面ABC,∠ =90°,
=90°,
方法1:空间向量法 如图建立空间直角坐标系 ,
,

因为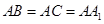 =4,
=4,
则
(I) ,
,
 ,∴
,∴ ,∴
,∴
 ,
∴
,
∴ ,∴
,∴
∵
 平面
平面 ∴
∴  ⊥平面
⊥平面 (5分)
(5分)
(II) 平面AEO的法向量为 ,设平面 B1AE的法向量为
,设平面 B1AE的法向量为
 , 即
, 即
令x=2,则
∴
∴二面角B1—AE—F的余弦值为 (10分)
(10分)
(Ⅲ)因为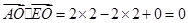 ,∴
,∴ , ∴
, ∴
∵ ,
,
∴ (14 分)
(14 分)
方法2:
依题意可知,  平面ABC,∠
平面ABC,∠ =90°,
=90°, ,∴
,∴
(I)∵ ,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
因为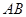 =
= ,则
,则 ,∴
,∴
∴B1O⊥EO,∴ ⊥平面
⊥平面 ;
(5分)
;
(5分)
(II)过O做OM⊥AE于点M,连接B1M,
∵B1O⊥平面AEO,可证B1M⊥AE,
∴∠B1MO为二面角B1—AE—O的平面角,
C1C⊥平面ABC,AO⊥OC,可证EO⊥AO,
在Rt△AEO中,可求 ,
,
在Rt△B1OM中,∠B1OM=90°,∴
∴二面角B1—AE—O的余弦值为 (10分)
(10分)
(Ⅲ)因为AB=AC,O为BC的中点,所以
又平面 平面
平面 ,且平面
,且平面 平面
平面 ,
,
所以 平面
平面 , 故
, 故 是三棱锥
是三棱锥 的高
的高
∴ (14分)
(14分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在A,B,C,D四小题中只能选做2题,每题10分,共计20分.
在A,B,C,D四小题中只能选做2题,每题10分,共计20分. (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. (2012•江苏一模)选做题
(2012•江苏一模)选做题 (2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,
(2012•徐州模拟)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,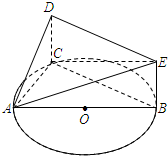 (2013•江门一模)如图,AB是圆O的直径,C是圆O上除A、B外的一点,△AED在平面ABC的投影恰好是△ABC.已知CD=BE,AB=4,
(2013•江门一模)如图,AB是圆O的直径,C是圆O上除A、B外的一点,△AED在平面ABC的投影恰好是△ABC.已知CD=BE,AB=4,