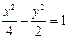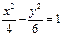题目内容
已知点F是双曲线
-
=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A.(1,+∞) | B.(1,2) | C.(1,1+
| D.(2,1+
|
根据双曲线的对称性,得
△ABE中,|AE|=|BE|,
∴△ABE是锐角三角形,即∠AEB为锐角
由此可得Rt△AFE中,∠AEF<45°,得|AF|<|EF|
∵|AF|=
=
,|EF|=a+c
∴
<a+c,即2a2+ac-c2>0
两边都除以a2,得e2-e-2<0,解之得-1<e<2
∵双曲线的离心率e>1
∴该双曲线的离心率e的取值范围是(1,2)
故选:B

△ABE中,|AE|=|BE|,
∴△ABE是锐角三角形,即∠AEB为锐角
由此可得Rt△AFE中,∠AEF<45°,得|AF|<|EF|
∵|AF|=
| b2 |
| a |
| c2-a2 |
| a |
∴
| c2-a2 |
| a |
两边都除以a2,得e2-e-2<0,解之得-1<e<2
∵双曲线的离心率e>1
∴该双曲线的离心率e的取值范围是(1,2)
故选:B


练习册系列答案
相关题目
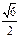 的是( )
的是( )