题目内容
已知命题p:在△ABC中,∠C>∠B是sinC>sinB的充分不必要条件,命题q:a>b是ac2>bc2的充分不必要条件则( )
| A、p 真q假 |
| B、p假q真 |
| C、“p 或q”为假 |
| D、“p且q”为真 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据充分条件和必要条件的定义集合复合命题之间的关系即可得到结论.
解答:
解:在△ABC中,∠C>∠B等价为c>b,根据正弦定理等价为sinC>sinB,故,∠C>∠B是sinC>sinB的充要条件,故p是假命题.
若c=0.当满足a>b时,ac2>bc2不成立,故a>b是ac2>bc2的充分不必要条件错误,故q是假命题.
则“p 或q”为假,
故选:C
若c=0.当满足a>b时,ac2>bc2不成立,故a>b是ac2>bc2的充分不必要条件错误,故q是假命题.
则“p 或q”为假,
故选:C
点评:本题主要考查充分条件和必要条件的判断以及复合命题之间的关系,比较基础.

练习册系列答案
相关题目
如图是某同学用于计算S=sin1+sin2+sin3+…+sin2012值的程序框图,则在判断框中填写( )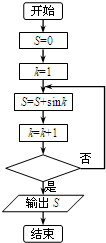

| A、k>2011? |
| B、k>2012? |
| C、k<2011? |
| D、k<2012? |
在等差数列{an}中,若a1,a4是方程x2-x-6=0的两根,则a2+a3的值为( )
| A、6 | B、-6 | C、-1 | D、1 |
若集合M={y|x2=y,x∈R},集合N={y|x+y=0,x∈R},则M∩N等于( )
| A、{y|y∈R} |
| B、{(-1,1),(0,0)} |
| C、{(0,0)} |
| D、{x|x≥0} |
在等差数列{an}中,若a4+a7=10,则{an}的前10项和为( )
| A、10 | B、20 | C、25 | D、50 |
已知函数f(x)=
则方程f(x)-a=0有四个实根的充要条件为( )
|
| A、a≥1 | B、a≤3 |
| C、1≤a≤3 | D、1<a<3 |