题目内容
12.已知函数f(x)满足f(x)=f(2-x),且x∈[-1,1]时,f(x)=1-x2,函数g(x)为偶函数,且x>0时,$g(x)=\frac{1}{x}$,则函数f(x)(x∈[-1,3])的图象与函数g(x-1)的图象的所有交点的横坐标之和等于( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
分析 确定函数f(x)关于直线x=1对称,函数g(x-1)的图象关于直线x=1对称,即可得出结论.
解答 解:∵函数f(x)满足f(x)=f(2-x),
∴函数f(x)关于直线x=1对称,
∵函数g(x)为偶函数,
∴函数g(x-1)的图象关于直线x=1对称,
∴函数f(x)(x∈[-1,3])的图象与函数g(x-1)的图象的所有交点的横坐标之和等于2×2=4.
故选:C.
点评 本题考查函数的奇偶性,考查函数图象的对称性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
7.函数$f(x)=\sqrt{1-x}+{2^x}$的定义域为( )
| A. | (0,1) | B. | (0,1] | C. | (-∞,1] | D. | [1,+∞) |
17.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:吨)的影响,为此对近6年的年宣传费x(单位:万元)和年销售量y(单位:吨)的数据进行整理,得如下统计表:
(Ⅰ)由表中数据求得线性回归方程$\hat y=\hat bx+\hat a$中的$\hat b≈0.6$,试求出$\hat a$的值;
(Ⅱ)已知这种产品的年利润z(单位:万元)与x、y之间的关系为z=30y-x2,根据(Ⅰ)中所求的回归方程,求年宣传费x为何值时,年利润z的预估值最大?
| x(万元) | 2 | 3 | 4.5 | 5 | 7.5 | 8 |
| y(吨) | 3 | 3.5 | 3.5 | 4 | 6 | 7 |
(Ⅱ)已知这种产品的年利润z(单位:万元)与x、y之间的关系为z=30y-x2,根据(Ⅰ)中所求的回归方程,求年宣传费x为何值时,年利润z的预估值最大?
4.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
(1)根据上面的数据判断,y=ax+b与y=$\frac{c}{x}$+d哪一个适宜作为产品销量y关于单价x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;(计算结果保留两位小数)
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$.
| 单价x(元) | 0.25 | 0.5 | 1 | 2 | 4 |
| 销量y(件) | 16 | 12 | 5 | 2 | 1 |
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;(计算结果保留两位小数)
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$.
1.已知实数a满足|a|<2,则事件“点M(1,1)与N(2,0)分别位于直线l:ax-2y+1=0两侧”的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{16}$ |
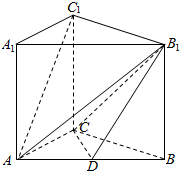 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.