题目内容
7. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,则当P运动时,A1P2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,则当P运动时,A1P2的最小值是( )| A. | 12-2$\sqrt{2}$ | B. | 12+2$\sqrt{2}$ | C. | 10+2$\sqrt{5}$ | D. | 10-2$\sqrt{5}$ |
分析 由已知得P点轨迹是以DC为直径位于平面ABCD内的半圆,取DC中点O,D1C1中点F,AB中点E,以O为原点,OE为x轴,OC为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出当P运动时,A1P2的最小值.
解答 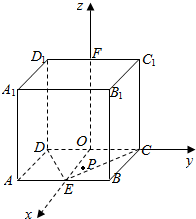 解:∵正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,
解:∵正方体ABCD-A1B1C1D1的棱长为2,P是底面ABCD内一动点,且满足PC⊥PD,
∴P点轨迹是以DC为直径位于平面ABCD内的半圆,
取DC中点O,D1C1中点F,AB中点E,
以O为原点,OE为x轴,OC为y轴,OF为z轴,建立空间直角坐标系,
则P(cosθ,sinθ,0),0≤θ≤2π,A1(2,-1,2),
∴$\overrightarrow{{A}_{1}P}$=(2-cosθ,-1-sinθ,2),
∴A1P2=${\overrightarrow{{A}_{1}P}}^{2}$=(2-cosθ)2+(-1-sinθ)2+4
=4-4cosθ+cos2θ+1+2sinθ+sin2θ+4
=10+2$\sqrt{5}$sin(θ+α),
∴当P运动时,A1P2的最小值是10-2$\sqrt{5}$.
故选:D.
点评 本题考查线段平方的最小值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连结DE.
如图,在△ABC中,∠C=90°,BC=8,AB=10,O为BC上一点,以O为圆心,OB为半径作半圆与BC边、AB边分别交于点D、E,连结DE.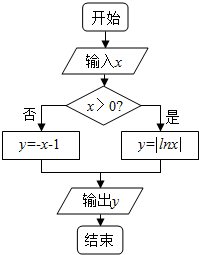 给出如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是2.
给出如图所示的流程图,若要使输入的x值与输出的y值相等,则这样的x值的个数是2.