题目内容
10.设a=${∫}_{1}^{{e}^{2}}$$\frac{1}{x}$dx,则二项式(x2-$\frac{a}{x}$)5的展开式中x的系数为( )| A. | 40 | B. | -40 | C. | 80 | D. | -80 |
分析 先求出定积分a的值,再利用二项展开式的通项公式,令x的指数等于1,求出r的值,即可计算结果.
解答 解:∵a=${∫}_{1}^{{e}^{2}}$$\frac{1}{x}$dx=lnx${|}_{1}^{{e}^{2}}$=lne2-ln1=2-0=2,
∴(x2-$\frac{a}{x}$)5=(x2-$\frac{2}{x}$)5的展开式的通项公式为:
Tr+1=${C}_{5}^{r}$•x2(5-r)•${(-\frac{2}{x})}^{r}$=${C}_{5}^{r}$•(-2)r•x10-3r,
令10-3r=1,解得r=3,
∴(x2-$\frac{a}{x}$)5的展开式中含x项的系数为
${C}_{5}^{3}$•(-2)3=-80.
故选:D.
点评 本题考查了定积分的计算问题,也考查了二项展开式的通项公式与二项式系数的计算问题,是基础题目.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.设A={x∈R|$\frac{1}{x}$≥1},B={x∈R|ln(1-x)≤0},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 必要不充分条件 |
5.已知i是虚数单位,则复数($\frac{1+i}{1-i}$)5的值为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |
20.设函数f(x)=alnx+bx2,若函数f(x)的图象在点(1,1)处的切线与y轴垂直,则实数a+b=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | -1 |
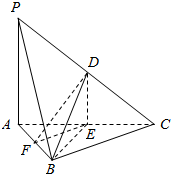 如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
如图所示,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.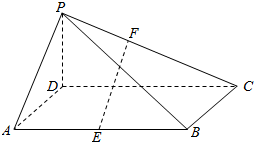 在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.
在如图所示的四棱锥中,底面ABCD是平行四边形,AB=4,BC=2,∠BCD=60°,且PD⊥底面ABCD,点E是AB的中点,点F是PC上一点.