题目内容

1．设A={x∈R|$\frac{1}{x}$≥1}，B={x∈R|ln（1-x）≤0}，则“x∈A”是“x∈B”的（　　）
A．充分不必要条件B．既不充分也不必要条件
C．充要条件D．必要不充分条件

分析 分别求出关于集合A、B中的x的范围，结合集合的关系，判断即可．

解答 解：A={x∈R|$\frac{1}{x}$≥1}={x|0＜x≤1}，
B={x∈R|ln（1-x）≤0}={x|0≤x＜1}，
则“x∈A”是“x∈B”的既不充分也不必要条件，
故选：B．

点评 本题考查了充分必要条件，考查解不等式问题，是一道基础题．

练习册系列答案
相关题目
11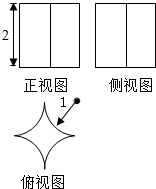．已知某几何体的三视图如图所示，其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆，则该几何体的表面积为（　　）
A．8-πB．8+πC．8-2πD．8+2π
12．设A={（x，y）|y=1+$\sqrt{4-{x}^{2}}$}，B={（x，y）|y=k（x-2）+4}，若A∩B中含有两个元素，则实数k的取值范围是（$\frac{5}{12}$，$\frac{3}{4}$]．
9．已知函数f（x）=$\frac{x}{1+|x|}$（x∈R），则下面的结论：
①该函数是奇函数；      ②该函数值域为（-1，1）；
③任取x1≠x2，都有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}$＞0； ④f（x）=x有三个根．
其中正确结论的序号为①②③．
16．已知函数f（x）=x2-4x+3，g（x）=mx+5-2m，
（1）求y=f（x）在区间[0，a]（a＞0）上的最小值
（2）若对任意的x1∈[1，4]，都有x2∈[1，4]，使f（x1）=g（x2）成立，求实数m的取值范围．
6．函数f（x）=lg（x-1）+lg（x+1）的单调区间是（　　）
A．（1，+∞）B．（0，+∞）C．（-∞，0）D．（-∞，-1）
13．求函数y=log${\;}_{\frac{1}{2}}$（x2-6x+8）的值域、单调区间．
10．设a=${∫}_{1}^{{e}^{2}}$$\frac{1}{x}$dx，则二项式（x2-$\frac{a}{x}$）5的展开式中x的系数为（　　）
A．40B．-40C．80D．-80
11．已知2-ai=b+i（a，b∈R），其中i为虚数单位，则a+b=（　　）
A．-1B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网