题目内容
已知二次函数f(x)=x2-mx+m-1.m∈R
(1)函数f(x)在区间(-1,1)上的最小值为g(m),求g(m)的解析式;
(2)求(1)中g(m)的最大值;
(3)若函数y=|f(x)|在[2,4]上单调递增,求实数m的取值范围.
(1)函数f(x)在区间(-1,1)上的最小值为g(m),求g(m)的解析式;
(2)求(1)中g(m)的最大值;
(3)若函数y=|f(x)|在[2,4]上单调递增,求实数m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)通过对m的讨论求出各个区间上g(m)的表达式,(2)由g(m)的表达式和m的取值范围求出即可.(3)由题意列出不等式组解出即可.
解答:
解:(1)由题意得:对称轴x=-
=
,
①当x=
≤-1,即m≤-2时,
g(m)=f(x)最小=f(-1)=1+m+m-1=2m;
②-1<
<1,即-2<m<2时,
g(m)=f(x)最小=f(
)=(
)2-m•
+m-1=-
+m-1;
③当
≥1,即m≥2时,
g(m)=f(x)最小=f(1)=1-m+m-1=0;
综合①②③得:
g(m)=
.
(2)当m≤-2时,g(m)最大=-4,
当-2<m<2时,g(m)=-
(m-2)2<0,无最大值;
当m≥2时,g(m)=0,
∴g(m)的最大值是:0.
(3)由题意得:
,
解得:m≤3.
或
,解得:m≥8.
∴m的范围是:(-∞,3]∪[8,+∞).
| -m |
| 2 |
| m |
| 2 |
①当x=
| m |
| 2 |
g(m)=f(x)最小=f(-1)=1+m+m-1=2m;
②-1<
| m |
| 2 |
g(m)=f(x)最小=f(
| m |
| 2 |
| m |
| 2 |
| m |
| 2 |
| m2 |
| 4 |
③当
| m |
| 2 |
g(m)=f(x)最小=f(1)=1-m+m-1=0;
综合①②③得:
g(m)=
|
(2)当m≤-2时,g(m)最大=-4,
当-2<m<2时,g(m)=-
| 1 |
| 4 |
当m≥2时,g(m)=0,
∴g(m)的最大值是:0.
(3)由题意得:
|
解得:m≤3.
或
|
∴m的范围是:(-∞,3]∪[8,+∞).
点评:本题考察了二次函数的性质,函数的最值问题,渗透了分类讨论思想,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
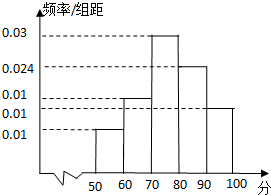 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.