题目内容
已知数列{an}的前n项和为Sn,且满足:Sn=n-an,
(1)求a1,a2,a3的值;
(2)求证:数列{an-1}是等比数列,并求{an}通项公式;
(3)令bn=(2-n)(an-1),(n=1,2,3…),如果对任意n∈N*,都有bn+
t≤t2,求实数t的取值范围.
(1)求a1,a2,a3的值;
(2)求证:数列{an-1}是等比数列,并求{an}通项公式;
(3)令bn=(2-n)(an-1),(n=1,2,3…),如果对任意n∈N*,都有bn+
| 1 |
| 4 |
考点:数列与不等式的综合,数列的应用
专题:函数的性质及应用,等差数列与等比数列
分析:(1)由已知中Sn=n-an,将n=1,2,3分别代入,可得a1,a2,a3的值;
(2)由已知可知:a1+a2+a3+…+an-1+an=n-an①,a1+a2+a3+…+an+an+1=n+1-an+1②,②-①可得2an+1-an=1,即:an+1-1=
(an-1),进而可得数列{an-1}是等比数列,结合a1-1=-
,可得{an}通项公式;
(3)由(2)可得an=1-(
)n,bn=
,进而求出bn的最大值,结合二次函数的图象和性质,可得实数t的取值范围.
(2)由已知可知:a1+a2+a3+…+an-1+an=n-an①,a1+a2+a3+…+an+an+1=n+1-an+1②,②-①可得2an+1-an=1,即:an+1-1=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(2)可得an=1-(
| 1 |
| 2 |
| n-2 |
| 2n |
解答:
解:(1)∵Sn=n-an,
∴S1=1-a1,
∴a1=
,
同理S2=2-a2,
∴a2=
,
S3=2-a3,
∴a3=
,
∴a1=
,a2=
,a3=
,…(3分)
证明:(2)由已知可知:a1+a2+a3+…+an-1+an=n-an①
a1+a2+a3+…+an+an+1=n+1-an+1②…(5分)
②-①可得2an+1-an=1…(6分)
即:an+1-1=
(an-1),又a1-1=-
…(8分)
所以数列{an-1}是以-
为首项,以
为公比的等比数列.
即an=1-(
)n…(10分)
解:(3)由(2)可得an=1-(
)n,bn=
由bn+1-bn=
-
=
=
>0,
可得n<3,
由bn+1-bn<0可得n>3,
所以 b1<b2<b3=b4>b5>…>bn>…,故bn有最大值b3=b4=
,
所以,对任意n∈N*,有bn≤
…(13分)
如果对任意n∈N*,都有bn+
t≤t2,即bn≤t2-
t成立,
则(bn)max≤t2-
t,
故有:
≤t2-
t,
解得t≥
或t≤-
.
所以实数t的取值范围是(-∞,-
]∪[
,+∞).…(16分)
∴S1=1-a1,
∴a1=
| 1 |
| 2 |
同理S2=2-a2,
∴a2=
| 3 |
| 4 |
S3=2-a3,
∴a3=
| 7 |
| 8 |
∴a1=
| 1 |
| 2 |
| 3 |
| 4 |
| 7 |
| 8 |
证明:(2)由已知可知:a1+a2+a3+…+an-1+an=n-an①
a1+a2+a3+…+an+an+1=n+1-an+1②…(5分)
②-①可得2an+1-an=1…(6分)
即:an+1-1=
| 1 |
| 2 |
| 1 |
| 2 |
所以数列{an-1}是以-
| 1 |
| 2 |
| 1 |
| 2 |
即an=1-(
| 1 |
| 2 |
解:(3)由(2)可得an=1-(
| 1 |
| 2 |
| n-2 |
| 2n |
由bn+1-bn=
| n+1-2 |
| 2n+1 |
| n-2 |
| 2n |
| n-1-2(n-2) |
| 2n+1 |
| 3-n |
| 2n+1 |
可得n<3,
由bn+1-bn<0可得n>3,
所以 b1<b2<b3=b4>b5>…>bn>…,故bn有最大值b3=b4=
| 1 |
| 8 |
所以,对任意n∈N*,有bn≤
| 1 |
| 8 |
如果对任意n∈N*,都有bn+
| 1 |
| 4 |
| 1 |
| 4 |
则(bn)max≤t2-
| 1 |
| 4 |
故有:
| 1 |
| 8 |
| 1 |
| 4 |
解得t≥
| 1 |
| 2 |
| 1 |
| 4 |
所以实数t的取值范围是(-∞,-
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查的知识点是数列,及数列的应用,(1)、(2)两问目标明确、思路清楚,第(3)问应是采用分离参数的方法解决恒成立问题,具体来说,就是解不等式(bn)max≤t2-
t.
| 1 |
| 4 |

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知平面点集M={(x,y)
},平面点集{(x,y)|x2+y2≤1},在集合M中任取一点P,则点P落在集合N中的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A,B两点,直线AF,BF分别与抛物线交于点C,D设直线AB,CD的斜率分别为k1,k2,则
等于( )
| k1 |
| k2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
若把函数 y=sin(x+
)的图象向右平移m(m>0)个单位长度后,得到y=sinx的图象,则m的最小值( )
| π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
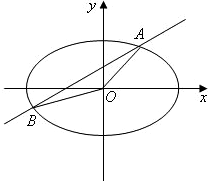 如图,直线y=x+b与椭圆
如图,直线y=x+b与椭圆