题目内容
若对于定义在R上的连续函数f(x),存在常数a(a∈R),使得f(x+a)+af(x)=0对任意的实数x都成立,则称f(x)是回旋函数,且阶数为a.
(Ⅰ)试判断函数f(x)=sinπx,g(x)=x2是否为阶数为1的回旋函数,并说明理由;
(Ⅱ)证明:函数h(x)=2x是回旋函数;
(Ⅲ)证明:若函数f(x)是一个阶数为a(a>0)的回旋函数,则函数f(x)在[0,2014a]上至少存在2014个零点.
(Ⅰ)试判断函数f(x)=sinπx,g(x)=x2是否为阶数为1的回旋函数,并说明理由;
(Ⅱ)证明:函数h(x)=2x是回旋函数;
(Ⅲ)证明:若函数f(x)是一个阶数为a(a>0)的回旋函数,则函数f(x)在[0,2014a]上至少存在2014个零点.
考点:抽象函数及其应用
专题:证明题,新定义,函数的性质及应用
分析:(Ⅰ)根据回旋函数的定义,一一加以判断,注意运用诱导公式和恒成立思想;
(Ⅱ)由定义可得2x+a+a•2x=0?2a=-a,则a<0,令m(x)=2x+x,运用零点存在定理,即可得证;
(Ⅲ)由定义得到f(x+a)=-af(x),由于a>0,由零点存在定理得,在区间(x,x+a)上必有一个零点令x=0,a,2a,3a,…,2013a,即可得到.
(Ⅱ)由定义可得2x+a+a•2x=0?2a=-a,则a<0,令m(x)=2x+x,运用零点存在定理,即可得证;
(Ⅲ)由定义得到f(x+a)=-af(x),由于a>0,由零点存在定理得,在区间(x,x+a)上必有一个零点令x=0,a,2a,3a,…,2013a,即可得到.
解答:
(Ⅰ)解:对于f(x)=sin(πx),sinπ(x+1)+sinπx=-sinπx+sinπx=0,
对任意实数x成立,所以f(x)=sin(πx)是1阶回旋函数.
对于g(x)=x2,则(x+1)2+x2=0对任意实数都不成立,故g(x)=x2不是1阶回旋函数.
(Ⅱ)证明:对于h(x)=2x,2x+a+a•2x=0?2a=-a,则a<0,
令m(x)=2x+x,m(-1)<0,m(0)>0,则方程必有一解a,且-1<a<0,
故函数h(x)=2x是回旋函数.
(Ⅲ)证明:若函数f(x)是一个阶数为a(a>0)的回旋函数,
则f(x+a)+af(x)=0对任意的实数x都成立,即有f(x+a)=-af(x),
由于a>0,则f(x+a)与f(x)异号,由零点存在定理得,在区间(x,x+a)上必有一个零点,
可令x=0,a,2a,3a,…,2013a,则函数f(x)在[0,2014a]上至少存在2014个零点.
对任意实数x成立,所以f(x)=sin(πx)是1阶回旋函数.
对于g(x)=x2,则(x+1)2+x2=0对任意实数都不成立,故g(x)=x2不是1阶回旋函数.
(Ⅱ)证明:对于h(x)=2x,2x+a+a•2x=0?2a=-a,则a<0,
令m(x)=2x+x,m(-1)<0,m(0)>0,则方程必有一解a,且-1<a<0,
故函数h(x)=2x是回旋函数.
(Ⅲ)证明:若函数f(x)是一个阶数为a(a>0)的回旋函数,
则f(x+a)+af(x)=0对任意的实数x都成立,即有f(x+a)=-af(x),
由于a>0,则f(x+a)与f(x)异号,由零点存在定理得,在区间(x,x+a)上必有一个零点,
可令x=0,a,2a,3a,…,2013a,则函数f(x)在[0,2014a]上至少存在2014个零点.
点评:本题是新定义题,关键是理解新定义,利用新定义时,应注意赋值法的运用,同时考查零点存在定理的运用,属于中档题.

练习册系列答案
相关题目
已知P(x,y)是曲线C:
+
=1上的动点,则z=x-2y的最大值为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
设集合A={a,b},集合B={5,log2(a+3)},若A∩B={2},则A∪B等于( )
| A、{2,5,7} |
| B、{-1,2,5} |
| C、{1,2,5} |
| D、{-7,2,5} |
在极坐标系中,点M(3,
)和点N(-3,
π)的位置关系是( )
| π |
| 3 |
| 2 |
| 3 |
| A、关于极轴所在直线对称 | ||
| B、重合 | ||
C、关于直线θ=
| ||
| D、关于极点对称 |
 某班有12名男生和18名女生参加综合素质测试,所得分数的茎叶图如图,若成绩在75分以上(包括75分)定义为“优秀”,成绩在75分以下(不包括75分)定义为“非优秀”.
某班有12名男生和18名女生参加综合素质测试,所得分数的茎叶图如图,若成绩在75分以上(包括75分)定义为“优秀”,成绩在75分以下(不包括75分)定义为“非优秀”.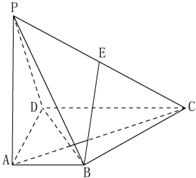 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.