题目内容
18.已知坐标平面上三点A(0,3),B(-$\sqrt{3}$,0),C($\sqrt{3}$,0),P是坐标平面上的点,且PA=PB+PC,则P点的轨迹方程为x2+(y-1)2=4(y≤0).分析 由题意画出图形,可得△ABC为正三角形,以C为顶点作正三角形PCD,利用三角形的边角之间的关系可得点P在△ABC的外接圆上.求出△ABC的外接圆的方程,结合已知PA>PB,PA>PC,求得P点轨迹.
解答 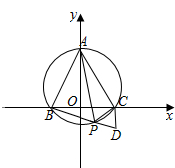 解:如图,由三点A(0,3),B(-$\sqrt{3}$,0),C($\sqrt{3}$,0),
解:如图,由三点A(0,3),B(-$\sqrt{3}$,0),C($\sqrt{3}$,0),
可得△ABC为正三角形,
以C为顶点作正三角形PCD,
由于△ABC也是正三角形,可证得△ACP≌△BCD,
∴BD=AP,又∵BD=PB+PC=PB+PD,
∴B、P、D三点共线.
∵∠CBP=∠PAC,
∴点P在△ABC的外接圆上.
又PA>PB,PA>PC,
∴点P的轨迹方程为:x2+(y-1)2=4(y≤0).
故答案为:x2+(y-1)2=4(y≤0).
点评 本题考查轨迹方程的求法,考查了学生灵活处理问题和解决问题的能力,训练了数形结合的解题思想方法,难度较大.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.已知正数x,y满足x+4y=4,则$\frac{x+28y+4}{xy}$的最小值为( )
| A. | $\frac{85}{2}$ | B. | 24 | C. | 20 | D. | 18 |
10.甲、乙两艘救助船相距1海里,经测量求救呼叫信号发出的位置与这两船构成的角度是救助船甲与救助船乙、求救呼叫信号发出的位置所构成角度的一半,可以判断三者构成的三角形是锐角三角形,则求救呼叫信号发出的位置与救助船乙的距离范围是( )
| A. | (1,2) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{3}$) | D. | ($\sqrt{2}$,$\sqrt{3}$) |