题目内容
6.已知函数f(x)=lnx+$\frac{a}{x}$(a≠0),试探究函数f(x)的极值情况.分析 求出函数的定义域,求出函数的导数,通过讨论a的范围,得到函数的单调区间,从而确定极值情况.
解答 解:f(x)的定义域是(0,+∞),
f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$,
a≤0时,f′(x)>0在(0,+∞)恒成立,
故f(x)在(0,+∞)递增;
函数f(x)无极值,
a>0时,令f′(x)>0,解得:x>a,
令f′(x)<0,解得;0<x<a,
∴f(x)在(0,a)递减,在(a,+∞)递增,
函数f(x)有极小值,
f(x)极小值=f(a)=1+lna.
点评 本题考查了函数的单调性、极值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
1.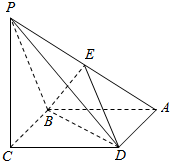 如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
(1)求证:平面EBD⊥平面ABCD;
(2)求二面角A-BE-D的大小.
 如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.
如图所示,已知四棱锥P-ABCD的底面是边长为a的菱形,且∠ABC=120°,PC⊥平面ABCD,PC=a,E为PA的中点.(1)求证:平面EBD⊥平面ABCD;
(2)求二面角A-BE-D的大小.
16.下列函数存在极值的是( )
| A. | y=$\frac{1}{x}$ | B. | y=x4 | C. | y=2 | D. | y=x3 |