题目内容
【题目】如图椭圆
的离心率为
， 其左顶点
在圆
上.
（1）求椭圆
的方程；
（2）直线
与椭圆的另一个交点为
，与圆
的另一个交点为
.是否存在直线，使得
？ 若存在，求出直线的斜率；若不存在，说明理由.
【答案】（1）
；（2）
.
【解析】
由顶点
在圆上可得
，再根据离心率公式可得
的值，结合
的关系，可求出
的值，然后得到所求的方程
联立直线与椭圆方程求出
，然后求得圆心到直线的距离，运用圆的弦长公式可得
，化简整理，即可判断是否存在
（1）因为椭圆
的左顶点在圆
上，所以.
又离心率为
，所以
，所以
,
所以
, 所以的方程为.
（2）（i）设点
，显然直线
存在斜率，
设直线的方程为
， 与椭圆方程联立得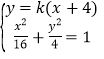
,
化简得到
，
因为
为上面方程的一个根，所以
，
所以
, 所以
圆心到直线的距离为
， 
.
因为
，
代入得到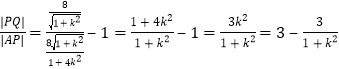
.
因为 
所以
.
练习册系列答案
相关题目
【题目】为了了解某省各景点在大众中的熟知度，随机对15～65岁的人群抽样了
人，回答问题“某省有哪几个著名的旅游景点？”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15，25） |
| 0．5 |
第2组 | [25，35） | 18 |
|
第3组 | [35，45） |
| 0．9 |
第4组 | [45，55） | 9 | 0．36 |
第5组 | [55，65] | 3 |
|
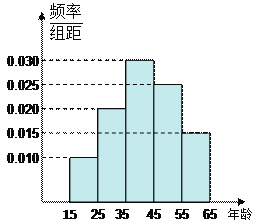
（1）分别求出
的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，求第2，3，4组每组各抽取多少人？
（3）在（2）抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．
