Question

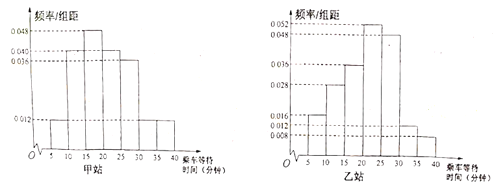
【题目】为评估大气污染防治效果，调查区域空气质量状况，某调研机构从两地分别随机抽取了天的观测数据，得到两地区的空气质量指数（AQI），绘制如图频率分布直方图：

根据空气质量指数，将空气质量状况分为以下三个等级：

空气质量指数（AQI）
空气质量状况	优良	轻中度污染	中度污染

（1）试根据样本数据估计地区当年（天）的空气质量状况“优良”的天数；

（2）若分别在两地区上述天中，且空气质量指数均不小于的日子里随机各抽取一天，求抽到的日子里空气质量等级均为“重度污染”的概率.

Answer 1

【答案】（1）274天（2）

【解析】

（1）从地区选出的20天中随机选出一天，这一天空气质量状况“优良”的频率为0.75，由估计地区当年天）的空气质量状况“优良”的频率为0.75，从而能求出地区当年天）的空气质量状况“优良”的天数．

（2）地20天中空气质量指数在，内为3个，设为，，，空气质量指数在，内为1个，设为，地20天中空气质量指数在，内为2个，设为，，空气质量指数在，内为3个，设为，，，设“，两地区的空气质量等级均为“重度污染””为，利用列举法能求出，两地区的空气质量等级均为“重度污染”的概率．

解：（1）从地区选出的天中随机选出一天，这一天空气质量状况“优良”的频率为，

估计地区当年（天）的空气质量状况“优良”的频率为，地区当年（天）的空气质量状况“优良”的天数约为天.

（2）地天中空气质量指数在内，为个，设为，空气质量指数在内，为个，设为，地天中空气质量指数在内，为个，设为，空气质量指数在内，为个，设为，设“两地区的空气质量等级均为“重度污染””为，则基本事件空间

基本事件个数为，，包含基本事件个数，

所以两地区的空气质量等级均为“重度污染”的概率为.