题目内容
已知圆的方程为
，若抛物线过点
，
且以圆的切线为准线，则抛物线的焦点的轨迹方程是
A． | B． |
C． | D． |
B
解析试题分析：抛物线上，到准线的距离
即到圆的切线的距离，由图形结合梯形中位线可得
，由抛物线定义可知
到抛物线焦点的距离之和等于4，即动点（焦点）到两定点的距离之和为4，大于间距离，符合椭圆定义，所以抛物线焦点的轨迹是以为焦点的椭圆（除去长轴端点），长轴为4，焦距为2，
，方程为
考点：抛物线定义，椭圆定义，直线与圆相切得位置关系
点评：此题难度较大，综合应用了椭圆，抛物线定义及直线和圆相切的性质
练习册系列答案
相关题目
若直线
经过点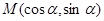
，则 （ ）
A． ． | B． ． |
C． ． | D． ． |
圆
的周长是（ ）
A． | B． | C． | D． |
若点P（3，－1）为圆
的弦AB的中点，则直线AB的方程为（ ）
| A．x+y-2=0 | B．2x－y-7=0 | C．2x+y-5=0 | D．x－y-4=0 |
已知集合
,
。若存在实数
使得
成立,称点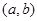
为“￡”点，则“￡”点在平面区域
内的个数是
| A．0 | B．1 | C．2 | D．无数个 |
圆
: 
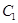与圆
: 
的位置关系是
| A．外离 | B．相交 | C．内切 | D．外切 |
圆
关于原点
对称的圆的方程为 ( )
A． | B． |
C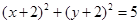． | D． |
若圆
：
关于直线
对称，则
的最小值是（ ）
| A．2 | B． | C． | D． |
若直线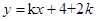
与曲线
有两个交点，则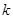
的取值范围是( )
A． | B． | C． | D． |