题目内容
已知A船在灯塔C北偏东85°且A到C的距离为2km，B船在灯塔C西偏北25°且B到C的距离为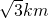
，则A，B两船的距离为
- A.
km - B.
km - C.
km - D.
km
D
分析：根据题意求得∠ACB=150°，再利用余弦定理求得AB的值．
解答：由题意可得∠ACB=（ 90°-25°）+85°=150°，又 AC=2，BC=
，
由余弦定理可得 AB2=AC2+BC2-2AC•BC•cos150°=13，∴AB=，
故选D．
点评：本题主要考查余弦定理的应用，求得∠ACB=150°，是解题的关键，体现了数形结合的数学思想，属于中档题．
分析：根据题意求得∠ACB=150°，再利用余弦定理求得AB的值．
解答：由题意可得∠ACB=（ 90°-25°）+85°=150°，又 AC=2，BC=
，由余弦定理可得 AB2=AC2+BC2-2AC•BC•cos150°=13，∴AB=
，故选D．
点评：本题主要考查余弦定理的应用，求得∠ACB=150°，是解题的关键，体现了数形结合的数学思想，属于中档题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
已知A船在灯塔C北偏东75°且A到C的距离为3km，B船在灯塔C西偏北15o且B到C的距离为
km，则A，B两船的距离为（ ）
| 3 |
| A、5km | ||
B、
| ||
| C、4km | ||
D、
|