题目内容
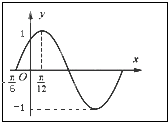
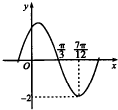 函数f(x)=Asin(ωx+?)(A,ω,?是常数,A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+?)(A,ω,?是常数,A>0,ω>0)的部分图象如图所示,下列结论:
①最小正周期为π;
②将f(x)的图象向左平移 个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④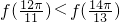 ;
;
⑤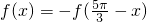 .
.
其中正确的是
- A.①②③
- B.②③④
- C.①④⑤
- D.②③⑤
C
分析:根据已知中函数y=Asin(ωx+?)(ω>0)的图象,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将( ,-2)代入解析式,可求出?值,进而求出函数的解析式,最后对照各选项进行判断即可.
,-2)代入解析式,可求出?值,进而求出函数的解析式,最后对照各选项进行判断即可.
解答:由图可得:函数函数y=Asin(ωx+?)的最小值-|A|=-2,
令A>0,则A=2,又∵ =
= -
- ,ω>0
,ω>0
∴T=π,ω=2,
∴y=2sin(2x+?)
将( ,-2)代入y=2sin(2x+?)得sin(
,-2)代入y=2sin(2x+?)得sin( +?)=-1
+?)=-1
即 +?=
+?= +2kπ,k∈Z
+2kπ,k∈Z
即?= +2kπ,k∈Z
+2kπ,k∈Z
∴f(x)=2sin(2x+ ).
).
∴f(0)=2sin =
= ,f(x+
,f(x+ )=2sin[2(x+
)=2sin[2(x+ )+
)+ ]=2sin(2x+
]=2sin(2x+ ).
).
f( )=2sin(
)=2sin( +
+ )=1.对称轴为直线x=
)=1.对称轴为直线x= ,一个对称中心是(
,一个对称中心是( ,0),故②③不正确;
,0),故②③不正确;
根据f(x)=2sin(2x+ )的图象可知,④
)的图象可知,④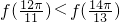 正确;
正确;
由于f(x)=2sin(2x+ )的图象关于点(
)的图象关于点( ,0)中心对称,故⑤
,0)中心对称,故⑤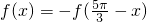 正确.
正确.
综上所述,其中正确的是①④⑤.
故选C.
点评:本题考查的知识点正弦型函数解析式的求法,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值.
分析:根据已知中函数y=Asin(ωx+?)(ω>0)的图象,可分析出函数的最值,确定A的值,分析出函数的周期,确定ω的值,将(
 ,-2)代入解析式,可求出?值,进而求出函数的解析式,最后对照各选项进行判断即可.
,-2)代入解析式,可求出?值,进而求出函数的解析式,最后对照各选项进行判断即可.解答:由图可得:函数函数y=Asin(ωx+?)的最小值-|A|=-2,
令A>0,则A=2,又∵
 =
= -
- ,ω>0
,ω>0∴T=π,ω=2,
∴y=2sin(2x+?)
将(
 ,-2)代入y=2sin(2x+?)得sin(
,-2)代入y=2sin(2x+?)得sin( +?)=-1
+?)=-1即
 +?=
+?= +2kπ,k∈Z
+2kπ,k∈Z即?=
 +2kπ,k∈Z
+2kπ,k∈Z∴f(x)=2sin(2x+
 ).
).∴f(0)=2sin
 =
= ,f(x+
,f(x+ )=2sin[2(x+
)=2sin[2(x+ )+
)+ ]=2sin(2x+
]=2sin(2x+ ).
).f(
 )=2sin(
)=2sin( +
+ )=1.对称轴为直线x=
)=1.对称轴为直线x= ,一个对称中心是(
,一个对称中心是( ,0),故②③不正确;
,0),故②③不正确;根据f(x)=2sin(2x+
 )的图象可知,④
)的图象可知,④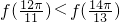 正确;
正确;由于f(x)=2sin(2x+
 )的图象关于点(
)的图象关于点( ,0)中心对称,故⑤
,0)中心对称,故⑤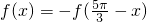 正确.
正确.综上所述,其中正确的是①④⑤.
故选C.
点评:本题考查的知识点正弦型函数解析式的求法,其中关键是要根据图象分析出函数的最值,周期等,进而求出A,ω和φ值.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
 如图所示的是定义域为R的函数f(x)=Asin(ωx+φ)(其中ω>0,φ∈[-π,π))的部分图象,则不等式
如图所示的是定义域为R的函数f(x)=Asin(ωx+φ)(其中ω>0,φ∈[-π,π))的部分图象,则不等式