题目内容
若方程|sinx|+cos|x|-a=0，在[-π，π]上有4个解，求a的取值范围．
【答案】分析：将a分离出来，得到a=|sinx|+cos|x|，若方程|sinx|+cos|x|-a=0，在[-π，π]上有4个解，
即函数y=a和y=|sinx|+cos|x|，x∈[-π，π]有4个交点即可．故问题转化为研究y=|sinx|+cos|x|，x∈[-π，π]的图象问题．因为函数中含有绝对值，故可分段讨论．
解答：解：|sinx|+cos|x|-a=0，在[-π，π]上有4个解
?a=|sinx|+cos|x|，x∈[-π，π]有4个交点
令y=|sinx|+cos|x|，x∈[-π，π]=
=
图象如图所示：
故a的取值范围是：1＜a＜
点评：本题考查方程根的个数问题，方程根的个数问题，往往转化为函数图象交点的个数问题．考查转化思想和数形结合思想．
即函数y=a和y=|sinx|+cos|x|，x∈[-π，π]有4个交点即可．故问题转化为研究y=|sinx|+cos|x|，x∈[-π，π]的图象问题．因为函数中含有绝对值，故可分段讨论．
解答：解：|sinx|+cos|x|-a=0，在[-π，π]上有4个解
?a=|sinx|+cos|x|，x∈[-π，π]有4个交点
令y=|sinx|+cos|x|，x∈[-π，π]=
=图象如图所示：
故a的取值范围是：1＜a＜
点评：本题考查方程根的个数问题，方程根的个数问题，往往转化为函数图象交点的个数问题．考查转化思想和数形结合思想．
练习册系列答案
阅读快车系列答案
相关题目
cosx+2a-1=0，在［0，π］上有两个不相等的实数根，则实数α的取值范围是( ） 
，2］ B.（
，2）
，
］ D.（-
，
］
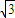sinx+cosx=a在[0，2π]上有两个不同的实数解x1、x2，求a的取值范围，并求x1+x2的值．