题目内容
若方程sinx-
cosx-m=0在x∈[0,π]上有解,则实数m的取值范围是
| 3 |
[-
,2]
| 3 |
[-
,2]
.| 3 |
分析:分类参数m,通过辅助角公式及三角函数的性质求解三角函数的范围,进而可求m的范围.
解答:解:∵sinx-
cosx-m=0
∴m=sinx-
cosx=2sin(x-
)
∵x∈[0,π]
∴x-
∈[-
,
]则sin(x-
)∈[-
,1]
∴2sin(x-
)∈[-
,2]
即实数m的取值范围是[-
,2]
故答案为:[-
,2]
| 3 |
∴m=sinx-
| 3 |
| π |
| 3 |
∵x∈[0,π]
∴x-
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| ||
| 2 |
∴2sin(x-
| π |
| 3 |
| 3 |
即实数m的取值范围是[-
| 3 |
故答案为:[-
| 3 |
点评:本题主要考查了方程的解的存在,以及三角函数的取值范围和性质,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
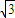 sinx+cosx=a在[0,2π]上有两个不同的实数解x1、x2,求a的取值范围,并求x1+x2的值.
sinx+cosx=a在[0,2π]上有两个不同的实数解x1、x2,求a的取值范围,并求x1+x2的值.