题目内容
设函数f(x)=ax2+bx+c,且f(1)=-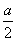 ,3a>2c>2b,求证:
,3a>2c>2b,求证:
(1)a>0,且-3< <-
<-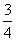 ;
;
(2)函数f(x)在区间(0,2)内至少有一个零点;
(3)设x1,x2是函数f(x)的两个零点,则 ≤|x1-x2|<
≤|x1-x2|<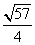 .
.
解析: (1)由已知得f(1)=a+b+c=-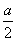 ,∴3a+2b+2c=0,
,∴3a+2b+2c=0,
又3a>2c>2b,∴a>0,b<0.
又2c=-3a-2b,∴3a>-3a-2b>2b,
∵a>0,∴-3< <-
<-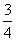 .
.
(2)由已知得f(0)=c,f(2)=4a+2b+c=a-c,
①当c>0时,f(0)=c>0,f(1)=-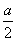 <0,
<0,
∴函数f(x)在区间(0,1)内至少有一个零点;
②当c≤0时,f(1)=-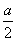 <0,f(2)=a-c>0,
<0,f(2)=a-c>0,
∴函数f(x)在区间(1,2)内至少有一个零点.
综上所述,函数f(x)在区间(0,2)内至少有一个零点.
(3)∵x1,x2是函数f(x)的两个零点,
∴x1+x2=- ,x1x2=
,x1x2=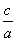 =-
=-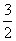 -
- ,
,
∴|x1-x2|=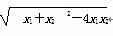
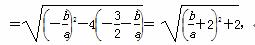
∵-3< <-
<-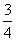 ,∴
,∴ ≤|x1-x2|<
≤|x1-x2|<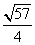 .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
已知集合A、B,定义集合A与B的一种运算A⊕B,其结果如下表所示:
| A | {1,2,3,4} | {-1,1} | {-4,8} | {-1,0,1} |
| B | {2,3,6} | {-1,1} | {-4,-2,0,2} | {-2,-1,0,1} |
| A⊕B | {1,4,6} | ∅ | {-2,0,2,8} | {-2} |
按照上述定义,若M={-2 011,0,2 012},N={-2 012,0,2 013},则M⊕N=________.
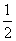 AB,求证:BN=2AM.
AB,求证:BN=2AM.
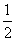 D.
D.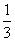
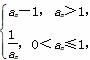 则下列结论中错误的是( )
则下列结论中错误的是( )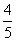 ,则a5=3 B.若a3=2,则m可以取3个不同的值
,则a5=3 B.若a3=2,则m可以取3个不同的值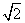 ,则数列{an}是周期为3的数列 D.∃m∈Q且m≥2,使得数列{an}是周期数列
,则数列{an}是周期为3的数列 D.∃m∈Q且m≥2,使得数列{an}是周期数列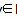 Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).
Z;②任意m,n∈N*,有f(m)f(n)=f(mn)+f(m+n-1).