Question

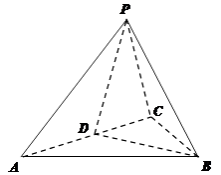
【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，且a＞b，a＞c．△ABC的外接圆半径为1， ，若边BC上一点D满足BD=2DC，且∠BAD=90°，则△ABC的面积为 ．

Answer 1

【答案】
【解析】解：∵△ABC的外接圆半径R为1， ， ∴由正弦定理 ，
可得：sinA= ，
∵边BC上一点D满足BD=2DC，
且∠BAD=90°，
∴A=120°，∠CAD=30°，
BD= a= ，CD= a= ，
∴如图，由正弦定理可得： ，可得：b= sin∠2= sin∠1= =c，
∴△BAC是等腰三角形，底角是30°，
∴sinB= ，可得：c=1，
∴S△ABC= = ．
所以答案是： ．

【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:．