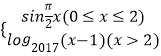题目内容
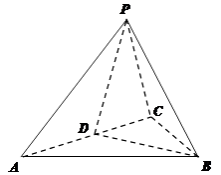
【题目】如图,在三棱锥 ![]() 中,
中, ![]() 是等边三角形,
是等边三角形, ![]() 是
是 ![]() 的中点,
的中点, ![]() ,二面角
,二面角 ![]() 的大小为
的大小为 ![]() .
.
(1)求证:平面 ![]() 平面
平面 ![]() ;
;
(2)求 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】
(1)解: 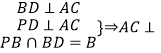 面
面 ![]()
又 ![]() 面
面 ![]() ,所以 面
,所以 面 ![]() 面
面 ![]()
即平面 ![]() 平面
平面 ![]()
(2)解:方法一:![]() 就是
就是 ![]() 的平面角,得
的平面角,得 ![]()
作 ![]() 于
于 ![]() , 连结
, 连结 ![]() ,则
,则 ![]() ,又
,又 ![]()
∴ ![]() 面
面 ![]() ,∴
,∴ ![]() 就是直线
就是直线 ![]() 与平面
与平面 ![]() 所成的角
所成的角
令 ![]() ,
, ![]() ,
, ![]()
∴ ![]()
方法二:![]() ,如图建立空间直角坐标系,
,如图建立空间直角坐标系,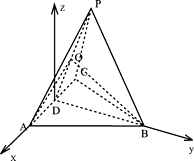
则 ![]() ,令
,令 ![]() , 则
, 则 ![]() ,
, ![]()
又 ![]() 为二面角
为二面角 ![]() 的平面角,得
的平面角,得 ![]()
设 ![]() ,则
,则 ![]()
设 ![]() 为面
为面 ![]() 的一法向量,则
的一法向量,则 ![]()
![]()
得 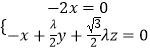 取
取 ![]() ,得
,得 ![]()
又 ![]() , 得
, 得 ![]()
设 ![]() 为平面
为平面 ![]() 所成角为
所成角为 ![]() , 则
, 则 ![]()
【解析】(1)证明AC⊥面PBD,即可证明平面PBD⊥平面PAC;
(2)求出面PAC的法向量,利用向量的方法求AB与平面PAC所成角的正弦值.
【考点精析】关于本题考查的用空间向量求直线与平面的夹角,需要了解设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: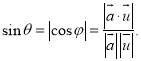 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目