题目内容

5．三角形ABC中，AB=2$\sqrt{3}$，BC=2，∠C=60°，则三角形ABC的面积为$2\sqrt{3}$．

分析 利用余弦定理可得AC，再利用三角形面积计算公式即可得出．

解答 解：三角形ABC中，设AC=x，由余弦定理可得：$（2\sqrt{3}）^{2}$=22+x2-2×2×xcos60°，
化为：x2-2x-8=0，
解得x=4．
∴S△ABC=$\frac{1}{2}×2×4sin6{0}^{°}$=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．

点评 本题考查了余弦定理、三角形面积计算公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
15．已知函数f（x）=$\left\{\begin{array}{l}{|x+a|，x≤0}\\{x+\frac{4}{x}+a，x＞0}\end{array}\right.$，若f（0）是该函数的最小值，则实数a的取值范围是[-2，0]．
16．从1，2，3，5这四个数字中任意选出两个数字，这两个数字之和是偶数的概率为（　　）
A．$\frac{2}{3}$B．$\frac{1}{2}$C．$\frac{1}{3}$D．$\frac{1}{6}$
13．函数f（x）=（$\frac{1}{4}$）x-（$\frac{1}{2}$）x-1，x∈[0，+∞）的值域为（　　）
A．（-$\frac{5}{4}$，1]B．[-$\frac{5}{4}$，-1]C．（-1，1]D．[-1，1]
20．春节期间，小王用私家车送4位朋友到三个旅游点去游玩，每位朋友在每一个景点下车的概率为$\frac{1}{3}$，用ξ表示4位朋友在第三个景点下车的人数，求：
（1）离散型随机变量ξ的概率分布；
（2）离散型随机变量ξ的均值．
10．执行如图所示的程序框图，则输出的y值为（　　）
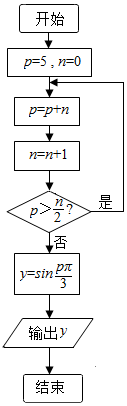
A．1B．0C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$
17．已知条件p：x≤0，条件q：$\frac{1}{x}$＞0，则￢p是q成立的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既非充分也非必要条件
14．设复数z1，z2在复平面内对应的点关于虚轴对称，且z1=2-i，则z1•$\overline{{z}_{2}}$=（　　）
A．-4+3iB．4-3iC．-3-4iD．-3+4i
15．设集合M={x|x≤0}，N={x|lnx≤1}，则下列结论正确的是（　　）
A．$N_≠^?M$B．M=NC．M∪∁RN=RD．M∩∁RN=M

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网