Question

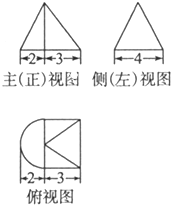
一个几何体的三视图如图所示，其侧（左）视图是一个等边三角形，则这个几何体的体积是

 

．

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知中的三视图可得该几何体是一个半圆锥和四棱锥的组合体，分别求出两个锥体底面面积和高，代入可得答案．

解答： 解：由已知中的三视图可得该几何体是一个半圆锥和四棱锥的组合体，
四棱柱的底面面积为3×4=12，
半圆锥的底面面积为

1

2

×π×22=2π，
两个锥体的高均侧视图的高，即2

3

，
故该组合体的体积V=

1

3

×（12+2π）×2

3

=8

3

+

4 3

3

π，
故答案为：8

3

+

4 3

3

π

点评：本题考查的知识点是由三视图求体积，其中根据已知的三视图判断出几何体的形状是解答的关键．