题目内容
已知函数 在
在 、
、 处分别取得极大值和极小值,记点
处分别取得极大值和极小值,记点 .
.
⑴求 的值;
的值;
⑵证明:线段 与曲线
与曲线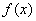 存在异于
存在异于 、
、 的公共点;
的公共点;
解法一:∵ ,依题意,
,依题意,
∴ ,(2分)
,(2分)
由 ,得
,得 (3分)
(3分)
令 ,
,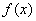 的单调增区间为
的单调增区间为 和
和 ,(5分)
,(5分)
 ,单调减区间为
,单调减区间为 (7分)
(7分)
所以函数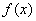 在
在 处取得极值。 故
处取得极值。 故 (9分)
(9分)
所以直线 的方程为
的方程为 (10分)
(10分)
由 得
得 w.w.w..c.o.m (11分)
w.w.w..c.o.m (11分)
令 ,易得
,易得 ,(13分)
,(13分)
而 的图像在
的图像在 内是一条连续不断的曲线,故
内是一条连续不断的曲线,故 在
在 内存在零点
内存在零点 ,这表明线段
,这表明线段 与曲线
与曲线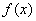 有异于
有异于 的公共点。(14分)
的公共点。(14分)
解法二:同解法一,可得直线 的方程为
的方程为 (10分)
(10分)
由 得
得 (11分)
(11分)
解得
 (13分)
(13分)
所以线段 与曲线
与曲线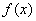 有异于
有异于 的公共点
的公共点 。
。

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,以
,以 为直径的圆与双曲线渐近线的一个交点为
为直径的圆与双曲线渐近线的一个交点为 ,则此双曲线的方程为
,则此双曲线的方程为 B.
B.  C.
C.  D.
D. 
 的最小值是2 B.
的最小值是2 B. 的最小值是2
的最小值是2  的最大值是
的最大值是
 ”是真命题,则实数
”是真命题,则实数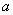 的取值范围为 .
的取值范围为 .  ,
, ,则
,则 ( )
( ) (B)
(B) (C)
(C) (D)
(D)
 的左、右焦点分别是
的左、右焦点分别是 ,过
,过 作倾斜角为
作倾斜角为 的直线交双曲线右支于
的直线交双曲线右支于 点,若
点,若 垂直于
垂直于 轴,则双曲线的离心率为( )
轴,则双曲线的离心率为( ) (B)
(B) (C)
(C) (D)
(D)
 满足
满足 则
则 的最大值为______.
的最大值为______. 的值为 ( )
的值为 ( )