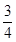题目内容
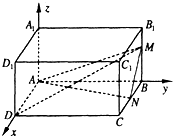 已知在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=3,M,N分别是棱BB1,BC上的点,且BM=2,BN=1,建立如图所示的空间直角坐标系.求:
已知在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=3,M,N分别是棱BB1,BC上的点,且BM=2,BN=1,建立如图所示的空间直角坐标系.求:(1)异面直线DM与AN所成角的余弦值;
(2)直线DM与平面AMN所成角的正弦值.
分析:(1)确定
=(-2,4,2),
=(1,4,0),利用向量的夹角公式,即可求异面直线DM与AN所成角的余弦值;
(2)求出平面AMN的一个法向量,利用向量的夹角公式,即可求直线DM与平面AMN所成角的正弦值.
| DM |
| AN |
(2)求出平面AMN的一个法向量,利用向量的夹角公式,即可求直线DM与平面AMN所成角的正弦值.
解答:解:由题意知,D(2,0,0),B(0,4,0),A1(0,0,3),M(0,4,2),N(1,4,0),
(1)
=(-2,4,2),
=(1,4,0),
∴cos?
,
>=
=
=
,…(5分)
∴异面直线DM与AN所成角的余弦值为
. …(7分)
(2)
=(0,4,2),
=(1,4,0),
设平面AMN的法向量为
=(x,y,z),
则
,即
,解得
,
不妨取x=4,则y=-1,z=2,故平面AMN的一个法向量为
=(4,-1,2),(10分)
则cos<
,
>=
=
=-
,…(12分)
根据图形可知,直线DM与平面AMN所成角的正弦值为
. …(14分)
(1)
| DM |
| AN |
∴cos?
| DM |
| AN |
| ||||
|
|
| -2×1+4×4+2×0 | ||||
2
|
7
| ||
| 102 |
∴异面直线DM与AN所成角的余弦值为
7
| ||
| 102 |
(2)
| AM |
| AN |
设平面AMN的法向量为
| m |
则
|
|
|
不妨取x=4,则y=-1,z=2,故平面AMN的一个法向量为
| m |
则cos<
| DM |
| m |
| ||||
|
|
| -2×4+4×(-1)+2×2 | ||||
2
|
2
| ||
| 21 |
根据图形可知,直线DM与平面AMN所成角的正弦值为
2
| ||
| 21 |
点评:本题考查向量知识的运用,考查空间角,考查学生的计算能力,正确运用向量的夹角公式是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
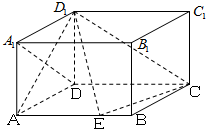 已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
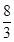 B.
B.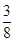 C.
C.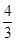 D.
D.