题目内容
 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.(Ⅰ)求证:平面ACC′A′⊥平面BDE;
(Ⅱ)若点P为棱C′D′的中点,点E为棱CC′的中点,求二面角P-BD-E的余弦值.
分析:(I)根据正方形的性质得到AC⊥BD,由CC'⊥平面ABCD得到BD⊥CC',从而证出BD⊥平面ACC'A',再根据面面垂直判定定理,即可得到平面ACC′A′⊥平面BDE;
(II)建立如图所示空间直角坐标系,可得B、D、E、P各点的坐标,从而得出
、
、
的坐标,利用垂直向量数量积为零的方法,建立方程组解出
=(1,-1,4)是平面BDE的一个法向量,
=(1,-1,1)是平面PBD的一个法向量,根据空间向量的夹角公式加以计算,即可得到二面角P-BD-E的余弦值.
(II)建立如图所示空间直角坐标系,可得B、D、E、P各点的坐标,从而得出
| DB |
| DE |
| DP |
| m |
| n |
解答:解:(Ⅰ)∵四边形ABCD为正方形,∴AC⊥BD,
∵CC'⊥平面ABCD,BD?平面ABCD,∴BD⊥CC'.
又∵CC'∩AC=C,∴BD⊥平面ACC'A'.
∵BD?平面BDE,
∴平面BDE⊥平面ACC'A',即平面ACC′A′⊥平面BDE;
(Ⅱ)建立分别以DA、DC、DD'为x轴、y轴和z轴,建立空间直角坐标系,如图所示.
可得D(0,0,0),B(2,2,0),E(0,2,
),P(0,1,1).
设平面BDE的一个法向量为
=(x,y,z),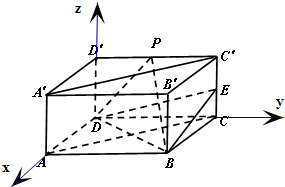
∵
=(2,2,0),
=(0,2,
),
∴
,取x=1,得y=-1且z=4.
可得
=(1,-1,4);
设平面PBD的一个法向量为
=(m,n,p),
∵
=(0,1,1),∴
取m=1,得n=-1且p=1,可得
=(1,-1,1).
∵cos<
,
>=
=
,且二面角P-BD-E是锐二面角,
∴二面角P-BD-E的余弦值为
.
∵CC'⊥平面ABCD,BD?平面ABCD,∴BD⊥CC'.
又∵CC'∩AC=C,∴BD⊥平面ACC'A'.
∵BD?平面BDE,
∴平面BDE⊥平面ACC'A',即平面ACC′A′⊥平面BDE;
(Ⅱ)建立分别以DA、DC、DD'为x轴、y轴和z轴,建立空间直角坐标系,如图所示.
可得D(0,0,0),B(2,2,0),E(0,2,
| 1 |
| 2 |
设平面BDE的一个法向量为
| m |

∵
| DB |
| DE |
| 1 |
| 2 |
∴
|
可得
| m |
设平面PBD的一个法向量为
| n |
∵
| DP |
|
取m=1,得n=-1且p=1,可得
| n |
∵cos<
| m |
| n |
| ||||
|
|
| ||
| 3 |
∴二面角P-BD-E的余弦值为
| ||
| 3 |
点评:本题在特殊的长方体中证明线面垂直、面面垂直,并求二面角的余弦之值.着重考查了长方体的性质、空间垂直位置关系的判断与证明、利用空间向量研究平面与平面所成角的大小等知识,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
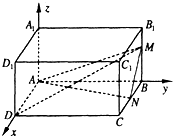 已知在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=3,M,N分别是棱BB1,BC上的点,且BM=2,BN=1,建立如图所示的空间直角坐标系.求:
已知在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=3,M,N分别是棱BB1,BC上的点,且BM=2,BN=1,建立如图所示的空间直角坐标系.求: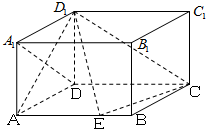 已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.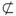
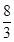 B.
B.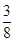 C.
C.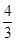 D.
D.