题目内容
如图,已知在长方体ABCD—A1B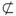
解析:∵B平面A1BCD1,BC
平面A1BCD1,
∴B
从而点B1到平面A1BCD1的距离即为所求.
过点B1作B1E⊥A1B于E,
∵BC⊥平面A1ABB1,且B1E
平面AA1B1B,
∴BC⊥B1E.
又BC∩A1B=B,
∴B1E⊥平面A1BCD1,
即线段B1E的长即为所求.
在Rt△A1B1B中,B1E=
,
∴直线B
.
答案:
练习册系列答案
相关题目
题目内容
如图,已知在长方体ABCD—A1B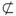
解析:∵B平面A1BCD1,BC平面A1BCD1,
∴B
从而点B1到平面A1BCD1的距离即为所求.
过点B1作B1E⊥A1B于E,
∵BC⊥平面A1ABB1,且B1E平面AA1B1B,
∴BC⊥B1E.
又BC∩A1B=B,
∴B1E⊥平面A1BCD1,
即线段B1E的长即为所求.
在Rt△A1B1B中,B1E=,
∴直线B.
答案:
已知如图：长方体ABCD-A1B1C1D1中，交于顶点A的三条棱长别为AD=3，AA1=4，AB=5．一天，小强观察到在A处有一只蚂蚁，发现顶点C1处有食物，于是它沿着长方体的表面爬行去获取食物，则蚂蚁爬行的最短路程是（ ）
a，M是AD的中点。
a，M、N分别是AD、BC的中点.
a,M是AD的中点. 
a，M、N分别是AD、BC的中点．