题目内容
利用定积分的几何意义或微积分基本定理计算下列定积分:
(1)∫01 dx=________. (2)∫132xdx=________.
dx=________. (2)∫132xdx=________.
解:(1)由定积分的几何意义知
∫01 dx是由曲线y=
dx是由曲线y= ,直线x=0,x=1围成的封闭图形的面积,
,直线x=0,x=1围成的封闭图形的面积,
故∫01 dx=
dx= ;
;
(2)∵(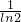 2x)′=2x
2x)′=2x
∴∫132xdx
= |13
|13
=
=
故答案为: ;
; .
.
分析:(1)本小题利用定积分的几何意义计算定积分,即求被积函数y= 与直线x=0,x=1所围成的图形的面积即可.
与直线x=0,x=1所围成的图形的面积即可.
(2)根据题意,直接找出被积函数 2x的原函数,直接计算在区间(1,3)上的定积分即可.
点评:本题主要考查定积分、定积分的几何意义、圆的面积等基础知识,考查考查数形结合思想.属于基础题.
∫01
 dx是由曲线y=
dx是由曲线y= ,直线x=0,x=1围成的封闭图形的面积,
,直线x=0,x=1围成的封闭图形的面积,故∫01
 dx=
dx= ;
;(2)∵(
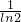 2x)′=2x
2x)′=2x∴∫132xdx
=
 |13
|13=

=

故答案为:
 ;
; .
.分析:(1)本小题利用定积分的几何意义计算定积分,即求被积函数y=
 与直线x=0,x=1所围成的图形的面积即可.
与直线x=0,x=1所围成的图形的面积即可.(2)根据题意,直接找出被积函数 2x的原函数,直接计算在区间(1,3)上的定积分即可.
点评:本题主要考查定积分、定积分的几何意义、圆的面积等基础知识,考查考查数形结合思想.属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 =
=
