题目内容
9. 某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形(如图所示的阴影部分).该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒(接缝用料忽略不计).问:
某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形(如图所示的阴影部分).该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒(接缝用料忽略不计).问:(1)包装盒的最大直径是多少?(精确到0.01厘米)
(2)画出你设计的剪裁图.
分析 (1)以正方形的中心为原点,建立坐标系,建立直线方程和圆的方程,数形结合求出满足条件的最大直径;
(2)根据(1)中解答思路,画出满足条件的裁剪图即可.
解答 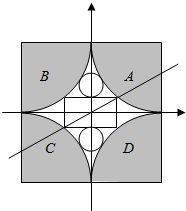 解:(1)建立如图所示的直角坐标系,
解:(1)建立如图所示的直角坐标系,
若使底面直径最大,应如图所示剪裁,
设底面半径为r,由圆柱形包装盒的底面直径和高相等,
可得AD=2r,AB=2πr,则A点的坐标为:(πr,r),
直线AC的方程为:y=$\frac{1}{π}$x,…①
位于第一象限的弧所在的圆的方程为(x-20)2+(y-20)2=202,…②,
将①代入②得:(πy-20)2+(y-20)2=202,
解得:y≈3.01cm,或y≈12.23cm(舍去),
即r的最大值为3.01cm,
即包装盒的最大直径是6.02cm.
(2)满足条件的剪裁图如图所示:
点评 本题考查的知识点是直线与圆的位置关系,建立恰当的坐标系,将形的问题化为数的问题,是解答的关键.

练习册系列答案
相关题目