题目内容
15.已知函数f(x)=log2(9x-a)-log2(3x-2),其中a为常数.(1)当a=5时,求不等式f(x)<2的解集;
(2)若不等式f(x)>1对定义域内的所有x恒成立,求a的取值范围.
分析 (1)由题意可得log2(9x-5)<log24(3x-2),即为9x-4•3x+3<0,且x>log95,运用指数不等式的解法,即可得到解集;
(2)不等式f(x)>1对定义域内的所有x恒成立,即log2(9x-a)-log2(3x-2)>1,运用对数函数的单调性,结合分离参数,二次函数的最值求法,函数恒成立思想即可得到所求a的范围.
解答 解:(1)当a=5时,f(x)=log2(9x-5)-log2(3x-2),
不等式f(x)<2,即为log2(9x-5)-log2(3x-2)<2,
log2(9x-5)<log24(3x-2),
即为9x-4•3x+3<0,且x>log95,
可得1<3x<3,且x>log95,
即为0<x<1且x>log95,
即不等式f(x)<2的解集为(log95,1).
(2)不等式f(x)>1对定义域内的所有x恒成立,
即log2(9x-a)-log2(3x-2)>1,
可得log2(9x-a)>log22(3x-2),
即有9x-a>2(3x-2)>0,
即为a<9x-2(3x-2),x>log32,
由9x-2(3x-2)=(3x-1)2+3,
由x>log32,可得9x-2(3x-2)>4,
则由题意可得a≤4,
则a的取值范围是(-∞,4].
点评 本题考查对数不等式的解法,函数恒成立问题的解法,注意运用运用对数函数的单调性,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.给出一个程序框如图,则输出x的值是( )


| A. | 45 | B. | 43 | C. | 41 | D. | 39 |
6.某几何体的三视图如图所示,则该三视图的体积为( )
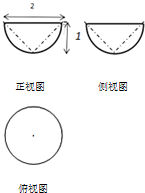

| A. | $\frac{π}{3}$ | B. | $\frac{4}{3}$π | C. | 2π | D. | $\frac{8}{3}$π |
3.△ABC中,角A,B,C的对边分别是a,b,c,已知a=b,c2=2b2(1-sinC),则C=( )
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |