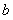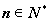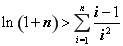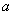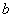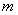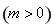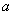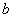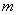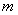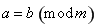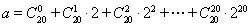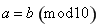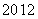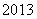题目内容
求经过极点O(0,0),A(6,
),B(6
,
)三点的圆的极坐标方程.
ρ=6
cos(θ-
)
【解析】将极坐标系内的问题转化为直角坐标系内的问题,
点O,A,B的直角坐标分别为(0,0),(0,6),(6,6),
故△OAB是以OB为斜边的等腰直角三角形,
进而易知圆心为(3,3),半径为3,
圆的直角坐标方程为(x-3)2+(y-3)2=18,
即x2+y2-6x-6y=0,
将x=ρcosθ,y=ρsinθ代入上述方程,得
ρ2-6ρ(cosθ+sinθ)=0,即ρ=6cos(θ-).
练习册系列答案
名校课堂系列答案
相关题目
