题目内容
1.甲、乙,丙3个盒中分别装有大小相等,形状相同的卡片若干张,甲盒中装有2张卡片,分别写有字母A和B;乙盒中装有3张卡片,分别写有字母C,D和E;丙盒中装有2张卡片,分别写有字母H和I,现要从3个盒中各随机取出1张卡片.求:(1)取出的3张卡片中恰好有1张、2张、3张写有元音字母的概率各是多少;(2)取出的3张卡片上全是辅音字母的概率.
分析 (1)作出树形图,由树形图,得所有可能出现的结果有12个,利用列举法能求出取出的3张卡片中恰好有1张、2张、3张写有元音字母的概率各是多少.
(2)满足全是辅音字母的结果有2个,由此能求出取出的3张卡片上全是辅音字母的概率.
解答 解:(1)作出树形图,如下: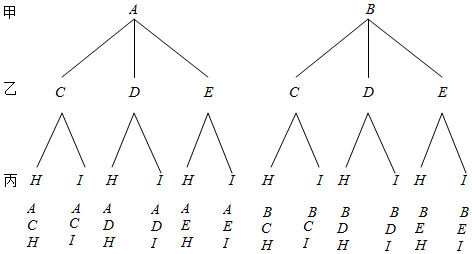
由树形图,得所有可能出现的结果有12个,它们出现的可能性相等,
其中满足只有一个元音字母的结果有5个,
∴取出的3张卡片中恰好有1张写有元音字母的概率p1=$\frac{5}{12}$;
其中满足只有两个元音字母的结果有4个,
∴取出的3张卡片中恰好有2张写有元音字母的概率p2=$\frac{4}{12}=\frac{1}{3}$;
其中满足三个元音字母的结果有1个,
∴取出的3张卡片中都写有元音字母的概率p3=$\frac{1}{12}$.
(2)满足全是辅音字母的结果有2个,
则取出的3张卡片上全是辅音字母的概率p=$\frac{2}{12}=\frac{1}{6}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
10.已知f(α)=$\frac{sin(π-α)cos(2π-α)}{sin(\frac{π}{2}+α)}$,则f($\frac{31π}{3}$)=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |