题目内容
2.若圆的方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),直线的方程为$\left\{\begin{array}{l}{x=t+1}\\{y=t-1}\end{array}\right.$(t为参数),则直线与圆的位置关系是( )| A. | 相离 | B. | 相交 | C. | 相切 | D. | 不能确定 |
分析 把圆的方程与直线的方程分别化为普通方程,求出圆心到直线的距离d,与半径比较大小即可得出.
解答 解:圆的方程为$\left\{\begin{array}{l}{x=2cosθ}\\{y=2sinθ}\end{array}\right.$(θ为参数),化为x2+y2=4,圆心O(0,0),半径r=2.
直线的方程为$\left\{\begin{array}{l}{x=t+1}\\{y=t-1}\end{array}\right.$(t为参数),化为x-y=2.
∴圆心到直线的距离d=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$<2=r,
∴直线与圆的位置关系是相交.
故选:B.
点评 本题考查了参数方程转化为普通坐标方程、点到直线的距离公式、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
13.已知函数f(x)=2x,若从区间[-2,2]上任取一个实数x,则使不等式f(x)>2成立的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.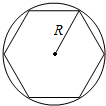 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )| A. | $\frac{3}{2π}$ | B. | $\frac{3\sqrt{3}}{2π}$ | C. | $\frac{3}{4π}$ | D. | $\frac{3\sqrt{3}}{4π}$ |
11.某市刑警队对警员进行技能测试,测试成绩分为优秀、良好、合格三个等级,测试结果如下表:(单位:人)
若按优秀、良好、合格三个等级分层,从中抽取40人,成绩为良好的有24人,则a等于( )
| 优秀 | 良好 | 合格 | |
| 男 | 40 | 105 | 25 |
| 女 | a | 15 | 5 |
| A. | 10 | B. | 15 | C. | 20 | D. | 30 |