题目内容
8．已知数列{an}的通项公式为an=n2-12n-13，则此数列的前n项和取最小时，n=12或13．分析 根据一元二次不等式的解法求出an=n2-12n-13≤0，即可得到结论．
解答 解：由an=n2-12n-13≤0，得-1≤n≤13，
即当n=13时，an=0，
当1≤n≤12时，an＜0，
当n≥14时，an＞0，
∴当n=12或13时，数列的前n项和取最小，
故答案为：12或13．
点评 本题主要考查数列和的最值的求解，解不等式是解决本题的关键．
练习册系列答案
相关题目
18．设A={x|y=$\sqrt{2-x}$}，B={x|y=ln（x2-1）}，则A∩∁UB=（ ）
| A． | {x|x＞-2} | B． | {x|1＜x≤2} | C． | {x|-1≤x≤1} | D． | ∅ |
19．直线x-2y+2=0和直线3x-y+7=0的夹角是（ ）
| A． | 30° | B． | 60° | C． | 45° | D． | 135° |
3．曲线y=cosx与x轴以及直线x=$\frac{3π}{2}$，x=0所围图形的面积为（ ）
| A． | 4 | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |
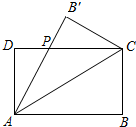春兰公司为一家制冷设备厂设计生产一种长方形薄板，其周长为4米，这种薄板须沿其对角线折叠后使用．如图所示，ABCD（AB＞AD）为长方形薄板，沿AC折叠后，AB′交DC于点P．当△ADP的面积最大时最节能．
17．某种产品的广告费支出x（单位：百万元）与销售额y（单位：百万元）之间有如下对应数据：
（1）求y关于x的回归直线方程．
（2）并预测广告费支出700万元的销售额大约是多少万元？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•\overline{{x}^{2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$）
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（2）并预测广告费支出700万元的销售额大约是多少万元？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n•\overline{{x}^{2}}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$•$\overline{x}$）