题目内容
【题目】已知![]() ,函数
,函数![]() .
.
(1)求证:曲线![]() 在点
在点![]() 处的切线过定点;
处的切线过定点;
(2)若![]() 是
是![]() 在区间
在区间![]() 上的极大值,但不是最大值,求实数
上的极大值,但不是最大值,求实数![]() 的取值范围;
的取值范围;
(3)求证:对任意给定的正数![]() ,总存在
,总存在![]() ,使得
,使得![]() 在
在![]() 上为单调函数.
上为单调函数.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)根据导数的几何意义可求得直线的斜率,从而得切线方程为![]() ,进而得切线过定点;(2)令
,进而得切线过定点;(2)令![]() 得
得![]() 或
或![]() ,
,![]() 是
是![]() 在区间
在区间![]() 上的极大值可得
上的极大值可得![]() 且
且![]()
![]() ,可得结果;(3)令
,可得结果;(3)令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减,若
递减,若![]() 在
在![]() 为单调函数,则
为单调函数,则![]() ,即
,即![]() .
.
试题解析:(1)![]() ,
,
![]() 曲线
曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]() ,令
,令![]() ,则
,则![]() ,
,
故曲线![]() 在点
在点![]() 处的切线过定点
处的切线过定点![]() .
.
(2)解:![]() .
.
令![]() 得
得![]() 或
或![]() .
.
![]() 是
是![]() 在区间
在区间![]() 上的极大值,
上的极大值,![]() .
.
令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减.
递减.
![]() 不是
不是![]() 在区间
在区间![]() 上的最大值,
上的最大值,
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
![]() ,又
,又![]() .
.
(3)证明:![]() .
.
![]() .
.
令![]() ,得
,得![]() 或
或![]() 递增;令
递增;令![]() ,得
,得![]() 递减.
递减.
![]() .
.
若![]() 在
在![]() 为单调函数,则
为单调函数,则![]() ,即
,即![]() .
.
故对任意给定的正数![]() ,总存在
,总存在![]() (其中
(其中![]() ),使得
),使得![]() 在
在![]() 上为单调函数.
上为单调函数.

【题目】某房屋开发公司根据市场调查,计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型 | 特大套 | 大套 | 经济适用房 |
舒适 | 100 | 150 |
|
标准 | 300 |
| 600 |
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求![]() ,
,![]() 的值;
的值;
(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房,该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
![]()
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】某企业生产的一种产品的广告费用![]() (单位:万元)与销售额
(单位:万元)与销售额![]() (单位:万元)的统计数据如下表:
(单位:万元)的统计数据如下表:
广告费用 |
|
|
|
|
|
销售额 |
|
|
|
|
|
(1)根据上述数据,求出销售额![]() (万元)关于广告费用
(万元)关于广告费用![]() (万元)的线性回归方程;
(万元)的线性回归方程;
(2)如果企业要求该产品的销售额不少于![]() 万元,则投入的广告费用应不少于多少万元?
万元,则投入的广告费用应不少于多少万元?
(参考数值: ![]() .
.
回归直线的斜率和截距的最小二乘法估计公式分别为: 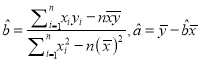 )
)