题目内容
解关于x的不等式
＜0 （a∈R）．
解：＜0?（x-a）（x-a2）＜0，
①当a=0或a=1时，原不等式的解集为Φ；
②当a＜0或a＞1时，a＜a2，此时a＜x＜a2；
③当0＜a＜1时，a＞a2，此时a2＜x＜a．
综上，当a＜0或a＞1时，原不等式的解集为{x|a＜x＜a2}；
当0＜a＜1时，原不等式的解集为{x|a2＜x＜a}；当a=0或a=1时，原不等式的解集为Φ．
分析：把不等式
转化为同解不等式，对a分类讨论解答即可．
点评：本题考查含有字母变量的不等式的解法，考查分类讨论思想，是中档题．
＜0?（x-a）（x-a2）＜0，①当a=0或a=1时，原不等式的解集为Φ；
②当a＜0或a＞1时，a＜a2，此时a＜x＜a2；
③当0＜a＜1时，a＞a2，此时a2＜x＜a．
综上，当a＜0或a＞1时，原不等式的解集为{x|a＜x＜a2}；
当0＜a＜1时，原不等式的解集为{x|a2＜x＜a}；当a=0或a=1时，原不等式的解集为Φ．
分析：把不等式
转化为同解不等式，对a分类讨论解答即可．点评：本题考查含有字母变量的不等式的解法，考查分类讨论思想，是中档题．
练习册系列答案
相关题目
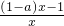＜0．
＜0 (a∈R).?
＜0．