题目内容
(本题满分13分)
设函数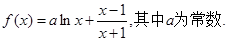
若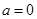 ,求曲线
,求曲线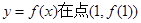 处的切线方程;
处的切线方程;
讨论函数 的单调性.
的单调性.
设函数
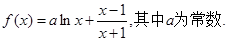
若
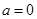 ,求曲线
,求曲线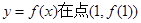 处的切线方程;
处的切线方程;讨论函数
 的单调性.
的单调性.(1) .
.
(2)当 时,函数
时,函数 在
在 上单调递增;
上单调递增;
当 时,函数
时,函数 在
在 上单调递减;
上单调递减;
当 时,
时, 在
在 ,
, 上单调递减,
上单调递减,
在 上单调递增.
上单调递增.
 .
.(2)当
 时,函数
时,函数 在
在 上单调递增;
上单调递增;当
 时,函数
时,函数 在
在 上单调递减;
上单调递减;当
 时,
时, 在
在 ,
, 上单调递减,
上单调递减,在
 上单调递增.
上单调递增.试题分析:(1)由题意知
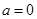 时,
时, ,求切线的斜率,即
,求切线的斜率,即 ,又
,又 ,由直线方程的点斜式进一步整理,得到切线方程为
,由直线方程的点斜式进一步整理,得到切线方程为 .
.(2)函数
 的定义域为
的定义域为 ,
, ,根据
,根据 的不同情况,讨论导函数值的正负,以确定函数的单调性.其中
的不同情况,讨论导函数值的正负,以确定函数的单调性.其中 时,情况较为单一,
时,情况较为单一, ,函数
,函数 在
在 上单调递增,
上单调递增,当
 时,令
时,令 ,
,由于
 ,再分
,再分 ,
, ,
, 等情况加以讨论.
等情况加以讨论.试题解析:(1)由题意知
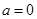 时,
时, ,
,此时
 ,
,可得
 ,又
,又 ,
,所以曲线
 在
在 处的切线方程为
处的切线方程为 .
.(2)函数
 的定义域为
的定义域为 ,
, ,
,当
 时,
时, ,函数
,函数 在
在 上单调递增,
上单调递增,当
 时,令
时,令 ,
,由于
 ,
,当
 时,
时, ,
, ,函数
,函数 在
在 上单调递减,
上单调递减,当
 时,
时, ,
, ,函数
,函数 在
在 上单调递减,
上单调递减,当
 时,
时, ,
,设
 是函数
是函数 的两个零点,
的两个零点,则
 ,
, ,
,由

 ,
,所以
 时,
时, ,函数
,函数 单调递减,
单调递减, 时,
时, ,函数
,函数 单调递增,
单调递增, 时,
时, ,函数
,函数 单调递减,
单调递减,综上可知,当
 时,函数
时,函数 在
在 上单调递增;
上单调递增;当
 时,函数
时,函数 在
在 上单调递减;
上单调递减;当
 时,
时, 在
在 ,
, 上单调递减,
上单调递减,在
 上单调递增.
上单调递增.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
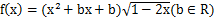 .
.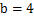 时,求
时,求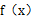 的极值;
的极值;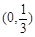 上单调递增,求b的取值范围.
上单调递增,求b的取值范围. ,且对任意实数x,总有
,且对任意实数x,总有 /(x)<3
/(x)<3 <3x-15的解集为( )
<3x-15的解集为( )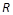 上可导的函数
上可导的函数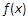 的图形如图所示,
的图形如图所示,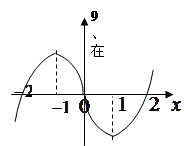 则关于
则关于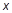 的不等式
的不等式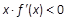 的解集为( ).
的解集为( ).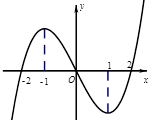




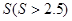 平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为
平方米的矩形场地的围墙,要求在前面墙的正中间留一个宽度为2米的出入口,后面墙长度不超过20米,已知后面墙的造价为每米45元,其它墙的造价为每米180元,设后面墙长度为x米,修建此矩形场地围墙的总费用为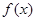 元.
元.
 在
在 上的最大值和最小值分别记为
上的最大值和最小值分别记为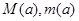 ,求
,求 ;
; 若
若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.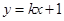 与曲线
与曲线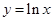 有公共点,则实数
有公共点,则实数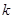 的取值范围是 .
的取值范围是 .