题目内容
如图,已知三棱锥 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段 上,且
上,且 ,
,

(1)证明:无论 取何值,总有
取何值,总有 .
.
(2)当 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段 上,且
上,且 ,
,
(1)证明:无论
 取何值,总有
取何值,总有 .
.(2)当
 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.(1)参考解析;(2)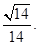
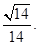
试题分析:(1)通过建立坐标系,写出相应的点的坐标,表示出向量
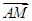 与向量
与向量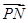 .通过计算向量
.通过计算向量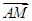 与向量
与向量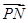 的数量积,即可得到结论.
的数量积,即可得到结论.(2)当
 时,要求平面
时,要求平面 与平面
与平面 所成锐二面角的余弦值,因为这两个平面的交线没画出来,所以用这两个平面的法向量的夹角的大小来表示. 平面
所成锐二面角的余弦值,因为这两个平面的交线没画出来,所以用这两个平面的法向量的夹角的大小来表示. 平面 的法向量较易表示,平面
的法向量较易表示,平面 的法向量要通过待定系数法求得.由于求锐二面角,所以求法向量的夹角的余弦值取正的即可.
的法向量要通过待定系数法求得.由于求锐二面角,所以求法向量的夹角的余弦值取正的即可.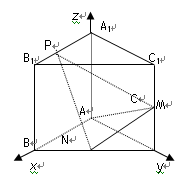
试题解析:以A为坐标原点,分别以
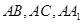 为
为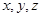 轴建立空间直角坐标系,
轴建立空间直角坐标系,则A1(0,0,2),B1(2,0,2), M(0,2,1),N(1,1,0),
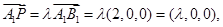
 ,
,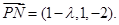
(1)∵
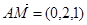 ,∴
,∴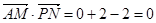 .
.∴无论
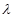 取何值,
取何值,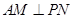 . 5分
. 5分(2)
 时,
时,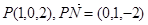 ,
, 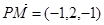 .
. 而面
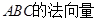
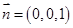 ,设平面
,设平面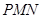 的法向量为
的法向量为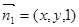 ,
,则
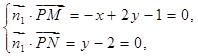
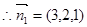 ,
,设
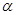 为平面
为平面 与平面ABC所成锐二面角,
与平面ABC所成锐二面角,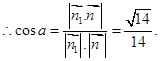
所以平面
 与平面
与平面 所成锐二面角的余弦值是
所成锐二面角的余弦值是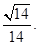 12分
12分
练习册系列答案
相关题目
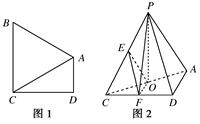
 为直角梯形,
为直角梯形, ,
, 平面
平面
 平面
平面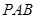 ;
; 所成锐二面角的余弦值.
所成锐二面角的余弦值.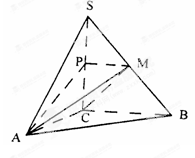
 的边长为4,
的边长为4, ,
, .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
 平面
平面 ;
;
 平面
平面 ;
; 的余弦值.
的余弦值. 的大小是60°,线段
的大小是60°,线段 在平面EFGH上,
在平面EFGH上, 在EF上,
在EF上, 所成的角的正弦值是__________.
所成的角的正弦值是__________.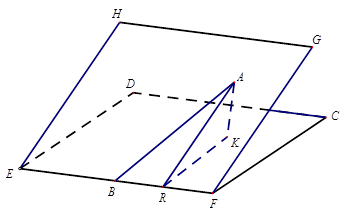
 ,
, 是两条不同的直线,
是两条不同的直线, 是一个平面,则下列命题正确的是 ( )
是一个平面,则下列命题正确的是 ( ) ,
,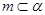 ,则
,则
 ,则
,则
 ,
, ,则
,则