题目内容
9.已知全集U=R,集合A={x|1<x<4},B={x|x≤3m-4或x≥8+m}(m<6)(1)若m=2,求A∩(∁UB)
(2)若A∩(∁UB)=∅,求实数m的取值范围.
分析 (1)求出m=2时集合B,再根据补集与交集的定义计算即可;
(2)求出∁UB,讨论∁UB是空集和非空集合时,求出满足条件的m取值范围.
解答 解:(1)全集U=R,集合A={x|1<x<4},B={x|x≤3m-4或x≥8+m}(m<6)
m=2时,B={x|x≤2或x≥10},
∴∁UB={x|2<x<10},
∴A∩(∁UB)={x|2<x<4};
(2)∁UB={x|3m-4<x<8+m},
当∁UB=∅时,3m-4≥8+m,解得m≥6,不合题意,舍去;
当∁UB≠∅时,应满足$\left\{\begin{array}{l}{m<6}\\{3m-4≥4}\end{array}\right.$或$\left\{\begin{array}{l}{m<6}\\{8+m≤1}\end{array}\right.$,
解得$\frac{8}{3}$≤m<6,m≤-7,
∴实数m的取值范围是m≤-7,或$\frac{8}{3}$≤m<6.
点评 本题考查了集合的定义、基本运算与应用问题,是基础题.

练习册系列答案
相关题目
1.设计一个计算1×3×5×7×9的算法,下面给出了算法语句的一部分,则在横线①上应填入下面数据中的( )

| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
20.下列关于命题的说法中错误的是( )
| A. | 对于命题p:?x∈R,使得x2+x+1<0,则¬P:?x∈R,均有x2+x+1≥0 | |
| B. | “x=1”是“x2-4x+3=0”的充分不必要条件 | |
| C. | 命题“若x2-4x+3=0,则x=1”的逆否命题为“若x≠1,则x2-4x+3≠0” | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
4.三棱锥的三条侧棱两两垂直,其长分别为$\sqrt{3},\sqrt{2},1$,则该三棱锥的外接球的表面积( )
| A. | 24π | B. | 18π | C. | 10π | D. | 6π |
1.过点P(1,0)与抛物线y=x2有且只有一个公共点的直线共有( )
| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
18.在△ABC中,角A、B、C所对的边长分别为a、b、c,$C=\frac{π}{3}$,若$\overrightarrow{OD}=a\overrightarrow{OE}+b\overrightarrow{OF}$,且D、E、F三点共线(该直线不经过O点),则△ABC周长的最小值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
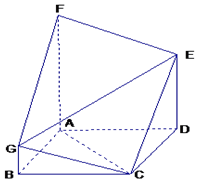 如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,
如图,多面体ABCDEFG中,四边形ABCD是正方形,FA⊥平面ABCD,