题目内容
已知直线l:kx-y+1-2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l交x轴正半轴于点A,交y轴正半轴于点B,O为坐标原点,且|OA|=|OB|,求k的值。
解:(1)证明:法一:直线l的方程可化为y-1=k(x-2),
故无论k取何值,直线l总过定点(2,1).…………6分
法二:设直线过定点(x0,y0),则kx0-y0+1-2k=0对任意k∈R恒成立,
即(x0-2)k-y0+1=0恒成立,
∴x0-2=0,-y0+1=0,
解得x0=2,y0=1,故直线l总过定点(2,1).…………6分
(2)因直线l的方程为y=kx-2k+1,
则直线l在y轴上的截距为1-2k,在x轴上的截距为2-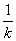 ,
,
依题意:1-2k=2-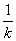 >0解得k=-1 或k=
>0解得k=-1 或k=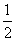 (经检验,不合题意)
(经检验,不合题意)
所以所求k=-1 …………12分

练习册系列答案
相关题目
 ”是“
”是“ ”的( )
”的( )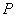 是双曲线
是双曲线 上一点,
上一点, 、
、 是双曲线的两个焦点,且
是双曲线的两个焦点,且 ,则
,则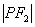 的值为( )
的值为( ) C.
C.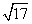 D.
D.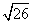
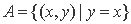 与集合
与集合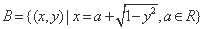 ,若
,若 的元素只有一个,则实数
的元素只有一个,则实数 的取值范围是( )
的取值范围是( ) B.
B. 或
或 或
或 D.
D. 或
或
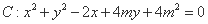 ,圆
,圆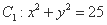 ,以及直线
,以及直线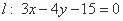 .
.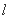 截得的弦长;
截得的弦长; 为何值时,圆
为何值时,圆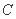 与圆
与圆 的公共弦平行于直线
的公共弦平行于直线 ;
; 中点到点
中点到点 距离等于弦
距离等于弦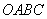 中,
中, 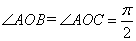 ,则
,则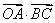 的值是( )
的值是( )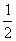 B.
B.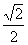 C.-
C.-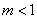 ”是“函数
”是“函数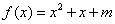 有零点”的( )
有零点”的( )  ,若
,若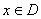 时,恒有
时,恒有 成立,则称函数
成立,则称函数 是
是 上
上  函数”.
函数”. 是定义域上的“
是定义域上的“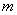 的取值范围;
的取值范围; 为
为 上的“
上的“ 与
与 的大小(其中
的大小(其中 );
); 的实数
的实数 ,
, ,
, ,…,
,…,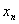 均有
均有 .
.