题目内容
16.若设“x,y>0,x+y>a,则$\frac{1+x}{y}$,$\frac{1+y}{x}$中至少有一个小于2”为真命题,则a的最小值是2.分析 将命题进行等价转化,作出不等式组对应的平面区域,利用线性规划的知识进行求解即可.
解答 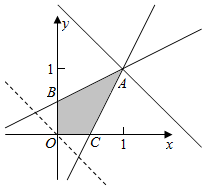 解:命题的等价条件是当x,y>0,$\frac{1+x}{y}$≥2,$\frac{1+y}{x}$≥2时,
解:命题的等价条件是当x,y>0,$\frac{1+x}{y}$≥2,$\frac{1+y}{x}$≥2时,
即$\left\{\begin{array}{l}{x,y>0}\\{1+x≥2y}\\{1+y≥2x}\end{array}\right.$时,x+y≤a恒成立,
作出不等式组对应的平面区域如图,
设z=x+y,则y=-x+z,
平移直线y=-x+z,当y=-x+z经过点A时,直线的截距最大,此时z最大,
由$\left\{\begin{array}{l}{1+x=2y}\\{1+y=2x}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$,即A(1,1),
此时z=1+1=2,
则a≥2,
即a的最小值是2,
故答案为:2
点评 本题主要考查命题真假的应用,根据条件转化为线性规划的知识进行求解是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
4.若函数f(x)=2x+2-x的定义域为R,则( )
| A. | f(x)为偶函数 | B. | f(x)为奇函数 | ||
| C. | f(x)既奇又偶函数 | D. | f(x)为非奇非偶函数 |
5.设集合M={0,2,-4,8},N={x|x是4的倍数},则M∩N=( )
| A. | {2,-4} | B. | {0,2,-4} | C. | {0,-4,8} | D. | {-4,8} |