题目内容
9.$\int_0^2{(\sqrt{4-{x^2}}+x)dx}$=π+2.分析 由和的积分等于积分的和展开,然后由定积分的几何意义求得${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx=π$,再求得${∫}_{0}^{2}xdx=\frac{1}{2}{x}^{2}{|}_{0}^{2}=2$,作和得答案.
解答 解:$\int_0^2{(\sqrt{4-{x^2}}+x)dx}$=${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx{+∫}_{0}^{2}xdx$,
令y=$\sqrt{4-{x}^{2}}$,得x2+y2=4(y≥0),
则圆x2+y2=4的面积为4π,
由定积分的几何意义可得,${∫}_{0}^{2}\sqrt{4-{x}^{2}}dx=π$,
又${∫}_{0}^{2}xdx=\frac{1}{2}{x}^{2}{|}_{0}^{2}=2$,
∴$\int_0^2{(\sqrt{4-{x^2}}+x)dx}$=π+2.
故答案为:π+2.
点评 本题考查定积分,考查定积分的几何意义,考查微积分基本定理的应用,是基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
17.下面的问题中必须用条件结构才能实现的个数是( )
①已知三角形三边长,求三角形的面积;②求方程ax+b=0,(a,b为常数)的根;③求三个实数a,b,c中的最大者;④求1+2+3+…+100的值.
①已知三角形三边长,求三角形的面积;②求方程ax+b=0,(a,b为常数)的根;③求三个实数a,b,c中的最大者;④求1+2+3+…+100的值.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.已知正数a1,a2,a3成等差数列,且其和为12;又a2,a3,a4成等比数列,其和为19,那么a4=( )
| A. | 12 | B. | 16 | C. | 9 | D. | 10 |
14.已知f(x)=x2-3,g(x)=mex,若方程f(x)=g(x)有三个不同的实根,则m的取值范围是( )
| A. | $(0,\frac{6}{e^3})$ | B. | $(-3,\frac{6}{e^3})$ | C. | $(-2e,\frac{6}{e^3})$ | D. | (0,2e) |
19.从集合A={-3,-2,-1,2}中随机选取一个数记为k,从集合B={-2,1,2}中随机选取一个数记为b,则直线y=kx+b不经过第四象限的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
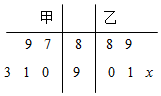 如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.
如图茎叶图记录了甲、乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为2.