题目内容
下面有五个命题:
①扇形的中心角为
,弧长为2π,则其面积为3π;
②终边在y轴上的角的集合是{a|a=
,k∈Z};
③已知角α 的终边经过点P(-5,12),则sinα+2cosα的值为
;
④函数y=sin(x-
)在(0,π)上是减函数;
⑤已知ω>0,函数f(x)=sin(ωx+
)在(
,π)上单调递减,则ω的取值范围是[
,
].
其中真命题的序号是______.
①扇形的中心角为
| 2π |
| 3 |
②终边在y轴上的角的集合是{a|a=
| kπ |
| 2 |
③已知角α 的终边经过点P(-5,12),则sinα+2cosα的值为
| 2 |
| 13 |
④函数y=sin(x-
| π |
| 2 |
⑤已知ω>0,函数f(x)=sin(ωx+
| π |
| 4 |
| π |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
其中真命题的序号是______.
①由弧长公式l=aR可得:α=
=(弧度),从而R=
=
=3.
由扇形的面积公式可得:S=
LR=
×2π×3=3π,故①正确.
②当k=2n(n为偶数)时,a=
=nπ,表示的是终边在x轴上的角,故②不正确;
③:∵x=-5,y=12,r=|OP|=13,∴sinα+2cosα=
+2×
=
.故③正确;
④∵函数y=sin(x-
)=-cosx,又函数y=cosx在区间(0,π)上单调递减,
∴函数y=sin(x-
)=-cosx在区间(0,π)是单调递增,故④不正确.
⑤ω(π-
)≤π?ω≤2,(ωx+
)∈[
ω+
,πω+
]?[
,
]
得:
ω+
≥
,πω+
≤
?
≤ω≤
.正确.
故答案为:①③⑤.
| L |
| R |
| L |
| α |
| 2π | ||
|
由扇形的面积公式可得:S=
| 1 |
| 2 |
| 1 |
| 2 |
②当k=2n(n为偶数)时,a=
| 2nπ |
| 2 |
③:∵x=-5,y=12,r=|OP|=13,∴sinα+2cosα=
| 12 |
| 13 |
| -5 |
| 13 |
| 2 |
| 13 |
④∵函数y=sin(x-
| π |
| 2 |
∴函数y=sin(x-
| π |
| 2 |
⑤ω(π-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
得:
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
故答案为:①③⑤.

练习册系列答案
相关题目
 ,弧长为2π,则其面积为3π;
,弧长为2π,则其面积为3π; ,k∈Z};
,k∈Z};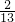 ;
; )在(0,π)上是减函数;
)在(0,π)上是减函数; )在(
)在( ,
, ].
].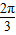 ,弧长为2π,则其面积为3π;
,弧长为2π,则其面积为3π;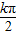 ,k∈Z};
,k∈Z};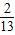 ;
;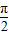 )在(0,π)上是减函数;
)在(0,π)上是减函数;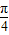 )在(
)在(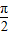 ,π)上单调递减,则ω的取值范围是[
,π)上单调递减,则ω的取值范围是[ ,
, ].
].