题目内容
下面有五个命题:
①扇形的中心角为 ,弧长为2π,则其面积为3π;
,弧长为2π,则其面积为3π;
②终边在y轴上的角的集合是{a|a= ,k∈Z};
,k∈Z};
③已知角α 的终边经过点P(-5,12),则sinα+2cosα的值为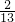 ;
;
④函数y=sin(x- )在(0,π)上是减函数;
)在(0,π)上是减函数;
⑤已知ω>0,函数f(x)=sin(ωx+ )在(
)在( ,π)上单调递减,则ω的取值范围是[
,π)上单调递减,则ω的取值范围是[ ,
, ].
].
其中真命题的序号是________.
①③⑤
分析:①由弧长公式α= 弧度可得半径R,由扇形的面积公式可得:S=
弧度可得半径R,由扇形的面积公式可得:S= LR;
LR;
②对k分奇数、偶数讨论即可;
③根据点P(-5,12)求出OP的长;再结合任意角的三角函数的定义即可求出结论.
④利用诱导公式先进行化简,进而可判断出是否正确.
⑤通过角的范围,直接推导ω的范围即可.
解答:①由弧长公式l=aR可得:α= =(弧度),从而R=
=(弧度),从而R= =
= =3.
=3.
由扇形的面积公式可得:S= LR=
LR= ×2π×3=3π,故①正确.
×2π×3=3π,故①正确.
②当k=2n(n为偶数)时,a= =nπ,表示的是终边在x轴上的角,故②不正确;
=nπ,表示的是终边在x轴上的角,故②不正确;
③:∵x=-5,y=12,r=|OP|=13,∴sinα+2cosα= +2×
+2× =
=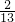 .故③正确;
.故③正确;
④∵函数y=sin(x- )=-cosx,又函数y=cosx在区间(0,π)上单调递减,
)=-cosx,又函数y=cosx在区间(0,π)上单调递减,
∴函数y=sin(x- )=-cosx在区间(0,π)是单调递增,故④不正确.
)=-cosx在区间(0,π)是单调递增,故④不正确.
⑤ω(π- )≤π?ω≤2,(ωx+
)≤π?ω≤2,(ωx+ )∈[
)∈[ ω+
ω+ ,πω+
,πω+ ]?[
]?[ ,
, ]
]
得: ω+
ω+ ≥
≥ ,πω+
,πω+ ≤
≤ ?
? ≤ω≤
≤ω≤ .正确.
.正确.
故答案为:①③⑤.
点评:本题考查了命题的真假判断与应用,综合考查了三角函数的单调性、扇形的面积公式,利用诱导公式进行化简等.
分析:①由弧长公式α=
 弧度可得半径R,由扇形的面积公式可得:S=
弧度可得半径R,由扇形的面积公式可得:S= LR;
LR;②对k分奇数、偶数讨论即可;
③根据点P(-5,12)求出OP的长;再结合任意角的三角函数的定义即可求出结论.
④利用诱导公式先进行化简,进而可判断出是否正确.
⑤通过角的范围,直接推导ω的范围即可.
解答:①由弧长公式l=aR可得:α=
 =(弧度),从而R=
=(弧度),从而R= =
= =3.
=3.由扇形的面积公式可得:S=
 LR=
LR= ×2π×3=3π,故①正确.
×2π×3=3π,故①正确.②当k=2n(n为偶数)时,a=
 =nπ,表示的是终边在x轴上的角,故②不正确;
=nπ,表示的是终边在x轴上的角,故②不正确;③:∵x=-5,y=12,r=|OP|=13,∴sinα+2cosα=
 +2×
+2× =
=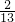 .故③正确;
.故③正确;④∵函数y=sin(x-
 )=-cosx,又函数y=cosx在区间(0,π)上单调递减,
)=-cosx,又函数y=cosx在区间(0,π)上单调递减,∴函数y=sin(x-
 )=-cosx在区间(0,π)是单调递增,故④不正确.
)=-cosx在区间(0,π)是单调递增,故④不正确.⑤ω(π-
 )≤π?ω≤2,(ωx+
)≤π?ω≤2,(ωx+ )∈[
)∈[ ω+
ω+ ,πω+
,πω+ ]?[
]?[ ,
, ]
]得:
 ω+
ω+ ≥
≥ ,πω+
,πω+ ≤
≤ ?
? ≤ω≤
≤ω≤ .正确.
.正确.故答案为:①③⑤.
点评:本题考查了命题的真假判断与应用,综合考查了三角函数的单调性、扇形的面积公式,利用诱导公式进行化简等.

练习册系列答案
相关题目
 的最小正周期是
的最小正周期是 ;
; |
| |;
|; 的图象和函数
的图象和函数 的图象有三个公共点;
的图象有三个公共点; 的图象向右平移
的图象向右平移 单位,得到
单位,得到 的图象;
的图象;
 上是减函数.
上是减函数.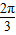 ,弧长为2π,则其面积为3π;
,弧长为2π,则其面积为3π;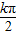 ,k∈Z};
,k∈Z};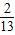 ;
;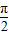 )在(0,π)上是减函数;
)在(0,π)上是减函数;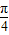 )在(
)在(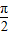 ,π)上单调递减,则ω的取值范围是[
,π)上单调递减,则ω的取值范围是[ ,
, ].
].