题目内容
点M(1,1)位于椭圆
+
=1内,过点M的直线与椭圆交于两点A、B,且M点为线段AB的中点,求直线AB的方程及
|AB|的值.
| x2 |
| 4 |
| y2 |
| 2 |
|AB|的值.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),代入椭圆的方程可得:
+
=1,
+
=1,两式相减可得:
+
=0,又x1+x2=2,y1+y2=2,
=k,即可解出k,可得直线AB的方程,把直线方程与椭圆方程联立可得根与系数的关系,利用弦长公式即可得出.
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 2 |
| y1-y2 |
| x1-x2 |
解答:
解:设A(x1,y1),B(x2,y2),代入椭圆的方程可得:
+
=1,
+
=1,
两式相减可得:
+
=0,
又x1+x2=2,y1+y2=2,
=k,
∴
+
=0,解得k=-
.
∴直线AB的方程为:y-1=-
(x-1),化为x+2y-3=0.
联立
,化为3x2-6x+1=0,
∴x1+x2=2,x1x2=
.
∴|AB|=
=
=
.
| ||
| 4 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
两式相减可得:
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 2 |
又x1+x2=2,y1+y2=2,
| y1-y2 |
| x1-x2 |
∴
| 2 |
| 4 |
| 2k |
| 2 |
| 1 |
| 2 |
∴直线AB的方程为:y-1=-
| 1 |
| 2 |
联立
|
∴x1+x2=2,x1x2=
| 1 |
| 3 |
∴|AB|=
| (1+k2)[(x1+x2)2-4x1x2] |
|
| ||
| 3 |
点评:本题考查了直线与椭圆相交问题转化为把直线方程与椭圆方程联立可得根与系数的关系、弦长公式、“点差法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
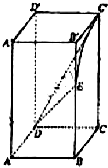 如图,四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=3
如图,四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=3| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
满足下列条件,能说明空间不重合的A,B,C三点共线的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、|
|
 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=