题目内容
 如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=
如图,四边形ABCD为菱形,ACFE为平行四边形,且面ACFE⊥面ABCD,AB=BD=2,AE=| 3 |
(Ⅰ)证明:CH⊥面BFE;
(Ⅱ)若AE与面ABCD所成的角为60°,求二面角B-EF-D的平面角余弦值的大小.
考点:直线与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离
分析:(Ⅰ)充分利用已知得到BD⊥平面ACFE,利用线面垂直的性质得到BD⊥CH,由等腰三角形的三线合一得到CH⊥FG,利用线面垂直的判定定理可证;
(Ⅱ)由平面ACFE⊥平面ABCD,得到∠EAC为AE与平面ABCD所成的角,进一步得到∠BMD为二面角B-EF-D的平面角,然后计算可得.
(Ⅱ)由平面ACFE⊥平面ABCD,得到∠EAC为AE与平面ABCD所成的角,进一步得到∠BMD为二面角B-EF-D的平面角,然后计算可得.
解答:
(Ⅰ)证明:∵四边形ABCD是菱形,
∴BD⊥AC又∵平面ACFE⊥平面ABCD,
∴BD⊥平面ACFE,∴BD⊥CH,
又∵H为FG的中点,CG=CF=
∴CH⊥FG又∵FG∩BD=G,
∴CH⊥平面BFD;
(Ⅱ)解:∵平面ACFE⊥平面ABCD,
∴E在平面ABCD内的射影落在AC上,
则∠EAC为AE与平面ABCD所成的角,∠EAC=60°,
过G作EF的垂线,垂足为M,连接MB,MD,MG,如图
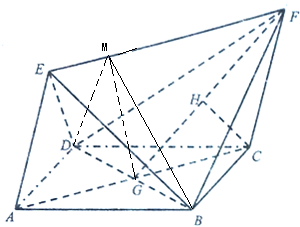
由(Ⅰ)得AC⊥平面BMD,∴EF⊥平面BMD,
∴∠BMD为二面角B-EF-D的平面角,
MG=
,BD=2,BG=1,BM=DM=
,
所以由余弦定理可得cos∠DMB=
.
∴BD⊥AC又∵平面ACFE⊥平面ABCD,
∴BD⊥平面ACFE,∴BD⊥CH,
又∵H为FG的中点,CG=CF=
| 3 |
∴CH⊥FG又∵FG∩BD=G,
∴CH⊥平面BFD;
(Ⅱ)解:∵平面ACFE⊥平面ABCD,
∴E在平面ABCD内的射影落在AC上,
则∠EAC为AE与平面ABCD所成的角,∠EAC=60°,
过G作EF的垂线,垂足为M,连接MB,MD,MG,如图

由(Ⅰ)得AC⊥平面BMD,∴EF⊥平面BMD,
∴∠BMD为二面角B-EF-D的平面角,
MG=
| 3 |
| 2 |
| ||
| 2 |
所以由余弦定理可得cos∠DMB=
| 5 |
| 13 |
点评:本题考查了线面垂直的判定定理的运用以及空间角的求法,关键是将空间角转化为平面角的问题解答,属于中档题

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若椭圆a2x2+y2=a2(0<a<1)上离顶点A(0,a)最远点为(0,-a),则( )
| A、0<a<1 | ||||
B、
| ||||
C、
| ||||
D、0<a<
|
tan(α+
)-tanα-
tanαtan(α+
)的值为( )
| π |
| 3 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|