题目内容
4.已知F为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a>0,b>0)的左焦点,定点G(0,c),若双曲线上存在一点P满足|PF|=|PG|,则双曲线的离心率的取值范围是( )| A. | ($\sqrt{2}$,+∞) | B. | (1,$\sqrt{2}$) | C. | [$\sqrt{3}$,+∞) | D. | (1,$\sqrt{3}$) |
分析 求出F的坐标,FG的中点和斜率,可得线段FG的垂直平分线方程,由题意可得FG的垂直平分线与双曲线有交点,运用渐近线的斜率可得-1>-$\frac{b}{a}$,再由离心率公式计算即可得到所求范围.
解答 解:由题意可得F(-c,0),FG的中点为(-$\frac{c}{2}$,$\frac{c}{2}$),
直线FG的斜率为$\frac{c-0}{0+c}$=1,可得FG的垂直平分线的斜率为-1,
即有线段FG的垂直平分线方程为y-$\frac{1}{2}$c=-(x+$\frac{1}{2}$c),即为y=-x.
由双曲线C上存在点P满足|PF|=|PG|,
可得FG的垂直平分线与双曲线有交点,
由双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即有-1>-$\frac{b}{a}$,即a<b,可得a2<b2=c2-a2,
可得e=$\frac{c}{a}$>$\sqrt{2}$,
故选:A.
点评 本题考查双曲线的方程和性质,考查离心率的范围的求法,以及线段的垂直平分线方程的求法,注意运用渐近线的斜率与直线的斜率的关系,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.双曲线C:$\frac{{x}^{2}}{3}$-y2=1的左右顶点分别为A1,A2,点P在双曲线C上,且直线PA1的斜率的取值范围为[1,2],那么直线PA2的斜率的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{1}{3}$] | B. | ($\frac{1}{6}$,$\frac{1}{3}$) | C. | [-$\frac{1}{3}$,-$\frac{1}{6}$] | D. | (-$\frac{1}{3}$,-$\frac{1}{6}$) |
12.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-y2=1(a>0)的离心率为$\sqrt{2}$,则其渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别是F1,F2,正三角形△AF1F2的顶点A在y轴上,边AF1与双曲线左支交于点B,且$\overrightarrow{A{F}_{1}}$=4$\overrightarrow{B{F}_{1}}$,则双曲线C的离心率的值是( )
| A. | $\frac{\sqrt{3}}{2}$+1 | B. | $\frac{\sqrt{13}+1}{3}$ | C. | $\frac{\sqrt{13}}{3}$+1 | D. | $\frac{\sqrt{3}+1}{2}$ |
14.在如图所示的流程图中,若输入a,b,c的值分别为2,4,5,则输出的x=( )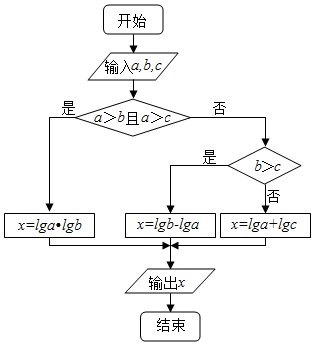

| A. | 1 | B. | 2 | C. | lg2 | D. | 10 |